Unsere optische Wahrnehmung neigt dazu Dinge zu sehen, die so nicht da sind.
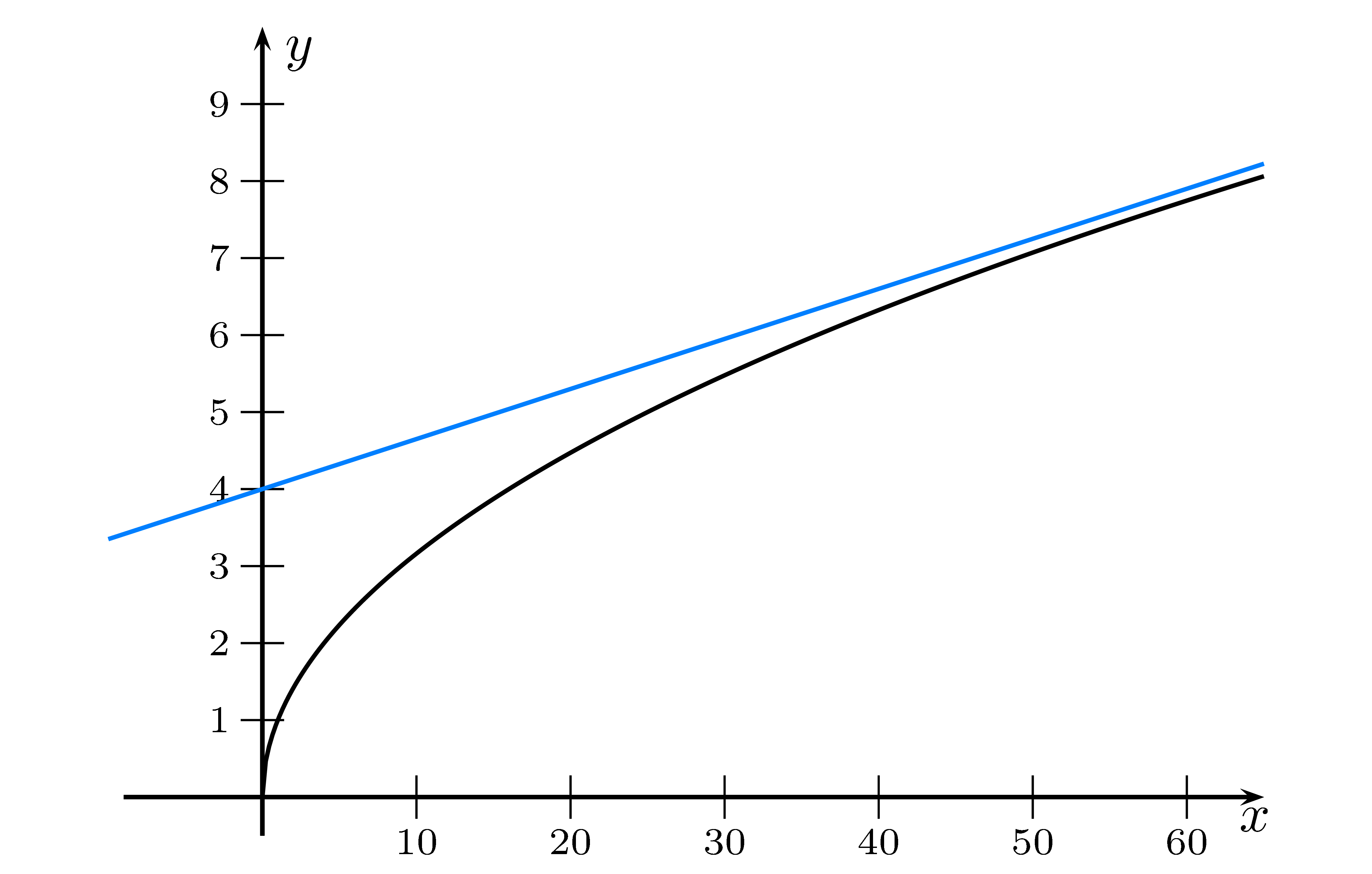
Im Schaubild ist der Graph der Wurzelfunktion $f(x)=\sqrt x$ dargestellt. Es erscheint so, als hätte der Graph eine Asymptote.
Dies liegt daran, dass unser Gehirn den Verlauf der Kurven verlängert.
Das heißt ein "das sieht man doch" ist kein mathematischer Beweis!
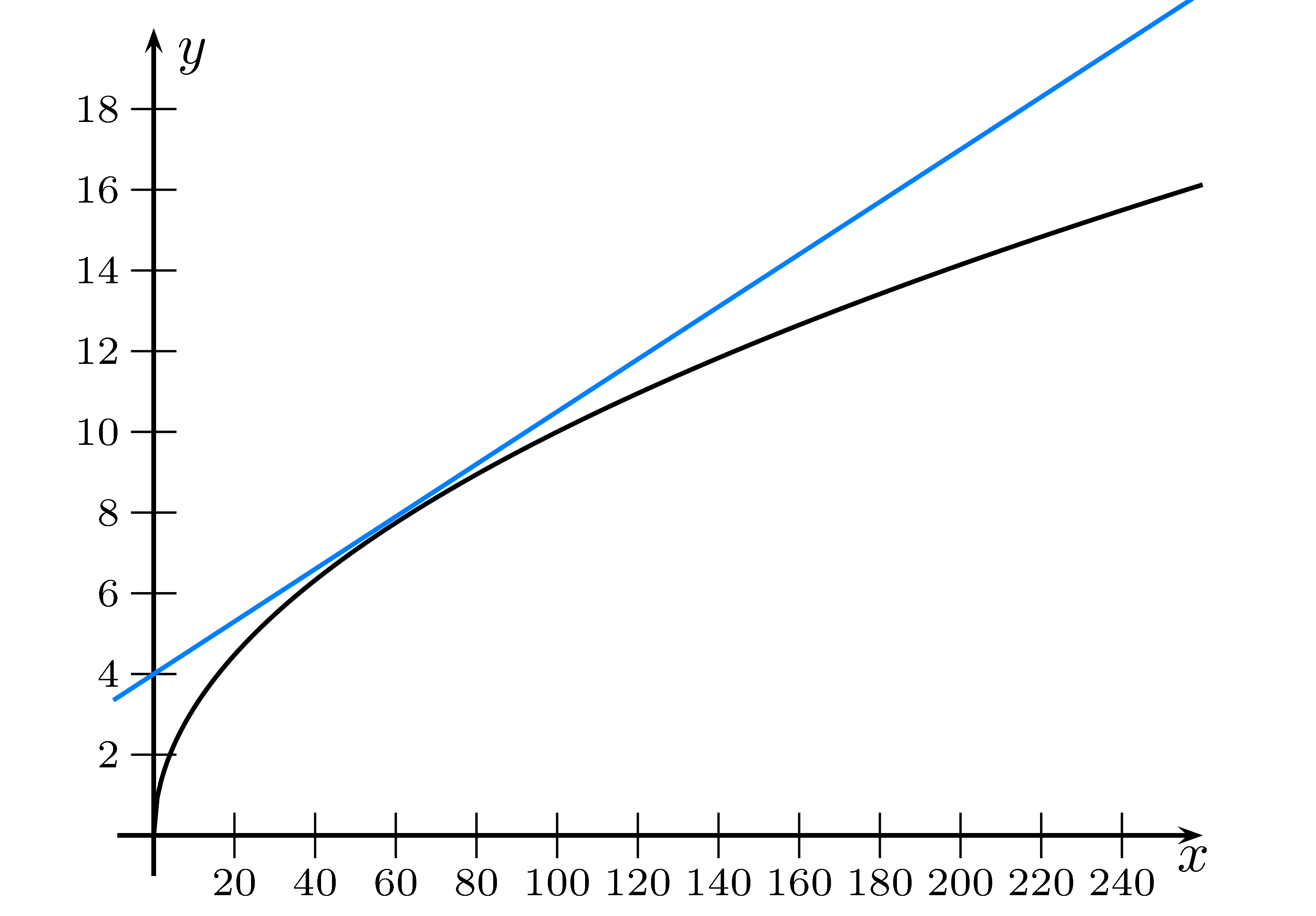
Im Schaubild ist der Graph der Wurzelfunktion $f(x)=\sqrt x$ dargestellt. Es erscheint so, als hätte der Graph eine Asymptote.
Dies liegt daran, dass unser Gehirn den Verlauf der Kurven verlängert.
Das heißt ein "das sieht man doch" ist kein mathematischer Beweis!