Ungleichungen lösen

Lösung mit Hilfe des Funktionsgraphen

Eine Ungleichung der Form $f(x) \lt 0$ (oder $f(x) \gt 0, f(x) \leq 0, f(x) \geq 0$) lässt sich mit Hilfe des Schaubilds $K_f$ der Funktion f lösen, indem man abliest, in welchen $x$-Bereichen $K_f$ oberhalb bzw. unterhalb der $x$-Achse verläuft.
Bei einer stetigen Funktion kann ein Vorzeichenwechsel (VZW) nur an einer Nullstelle erfolgen.
Deshalb genügt es die Nullstellen der Funktion zu kennen und zu wissen, ob an der jeweiligen Nullstelle ein Vorzeichenwechsel stattfindet oder nicht.
Oder man prüft für einen $x$-Wert zwischen zwei benachbarten Nullstellen das Vorzeichen eines Funktionswertes.

Beispiel 1
Löse $x^3-9x\lt 0$

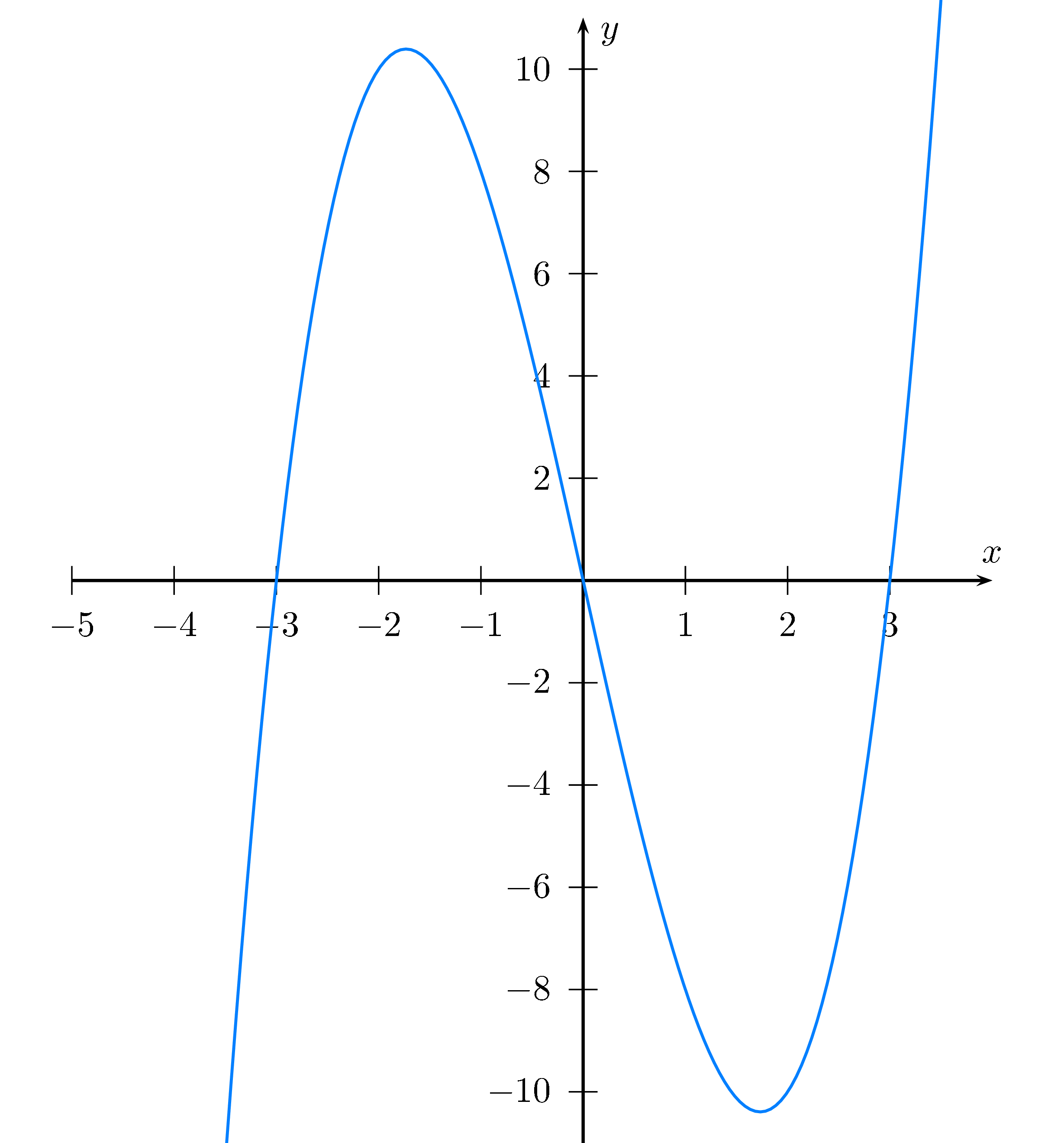
Die Funktion $f(x)=x^3-9x= x(x^2-9)=x(x-3)(x+3)$
hat drei einfache Nullstellen bei $x_1=-3, x_2=0$ und $x_3=3$.
Da $f(x)$ stetig ist und alle Nullstellen einfach sind, findet an jeder Nullstelle ein VZW statt.
Der Graph von $f(x)$ läuft von links unten nach rechts oben. Somit ist er negativ für $x\lt -3$, positiv für $-3\lt x\lt 0$, negativ für $0\lt x\lt 3$ und positiv für $x\gt 3$.
Die Lösungsmenge ist somit $\mathbb L = \{x\mid x\lt -3 \wedge x\in\mathbb R\} \cup \{x\mid 0\lt x \lt 3\}$
Als Intervalle geschrieben: $\mathbb L =]-\infty;\,-3[ \;\cup\; ]0;\,3[$

Der Graph von x hoch 3 minus 9 x — Der Graph von $f(x)=x^3-9x$

Beispiel 2
Löse $-x^3+4x^2\leq 0$

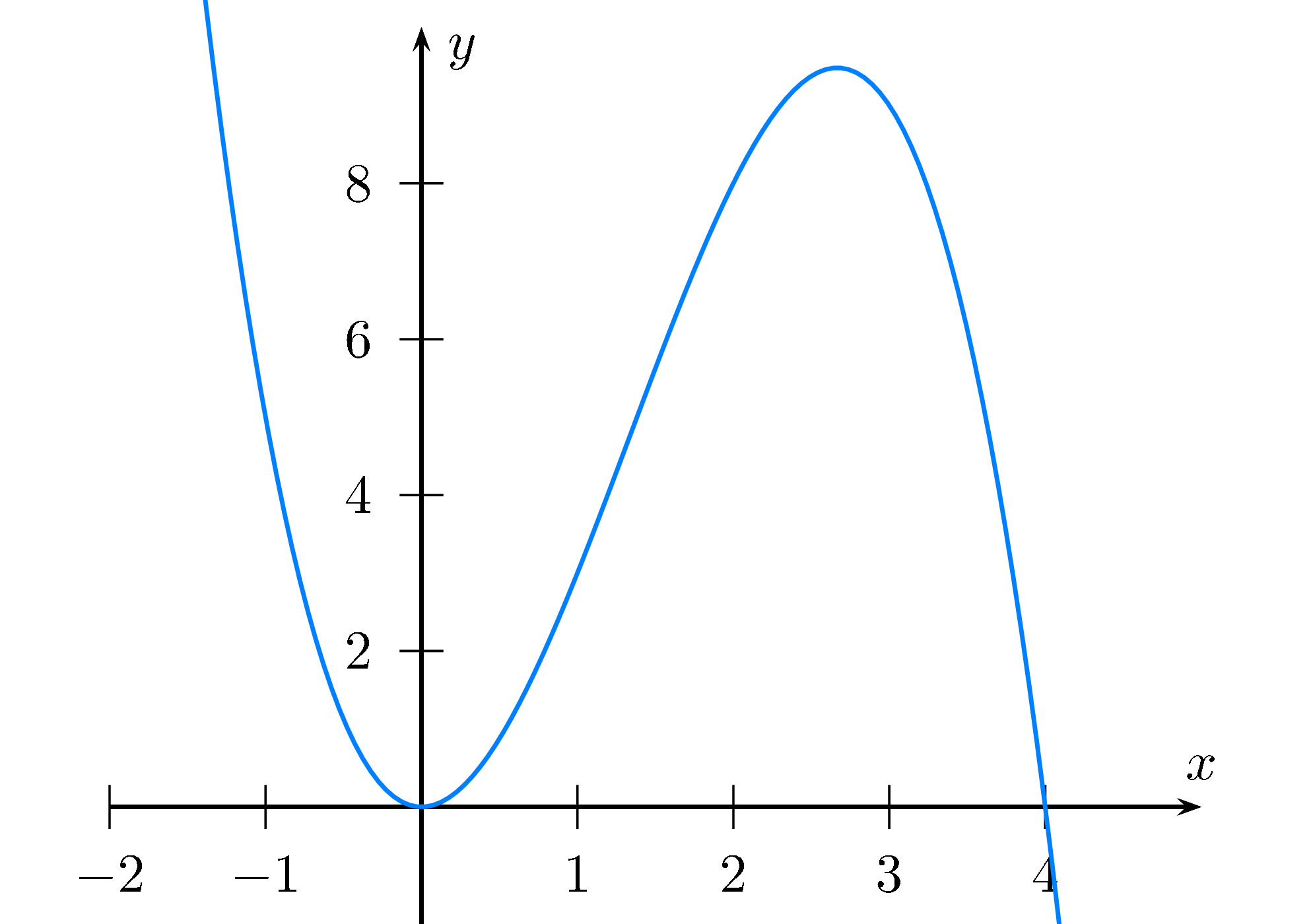
Die Funktion $f(x)=-x^3+4x^2= x^2(-x+4)$
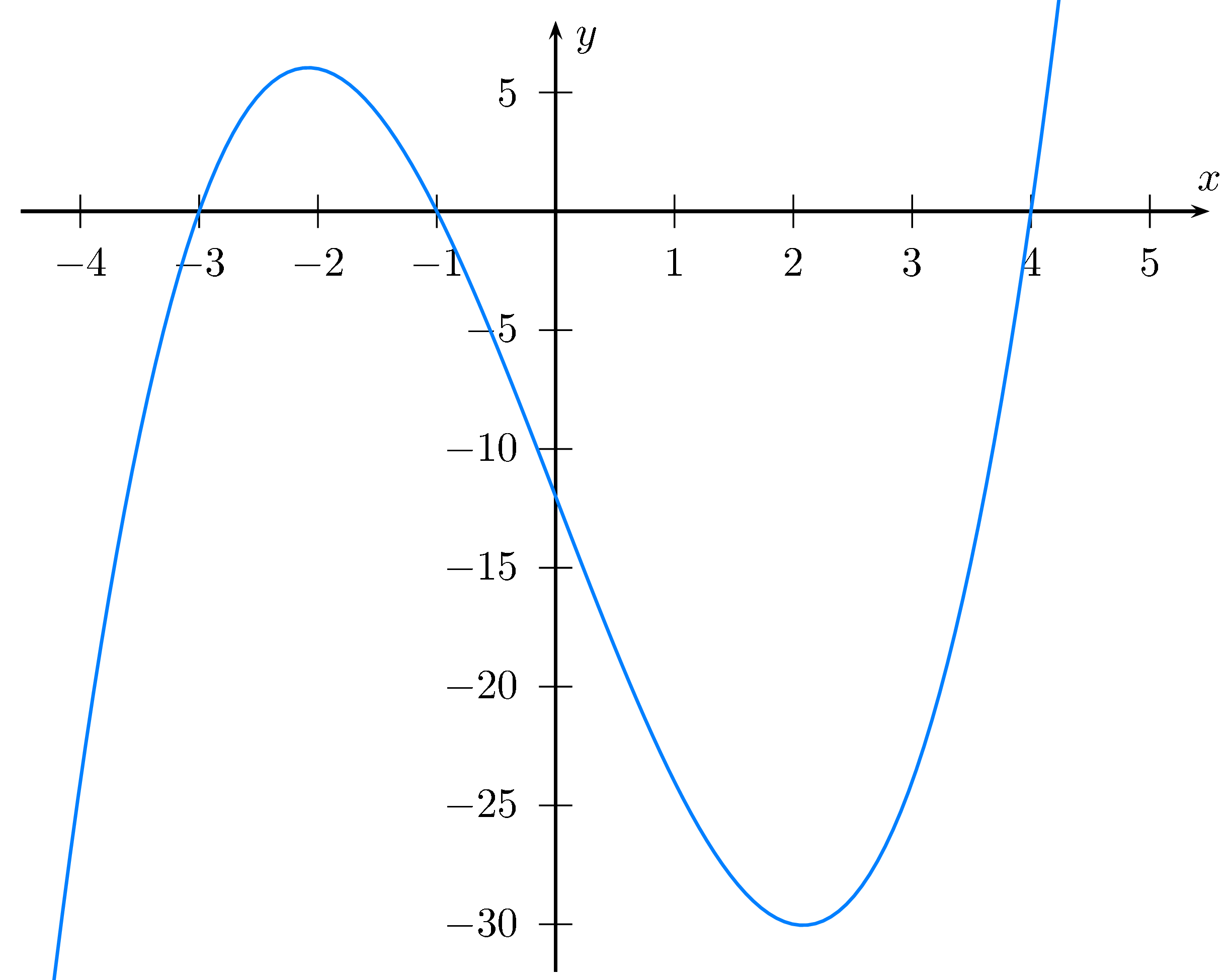
hat eine doppelte Nullstelle bei $x_1=0$ und eine einfache Nullstelle bei $x_2=4$.
Da $f(x)$ stetig ist findet nur bei $x_2$ ein VZW statt.
Der Graph von $f(x)$ läuft von links oben nach rechts unten.
Somit ist er positiv für $x\lt 0$ und $0\lt x\lt 4$, bei $x=0$ und $x=4$ ist er 0 und für $x\gt 4$ ist er negativ.
Die Lösungsmenge ist somit $\mathbb L = \{x\mid x\gt4 \wedge x\in\mathbb R\} \cup \{0\}$
Als Intervalle geschrieben: $\mathbb L =[4;\,\infty[ \;\cup\; [0;\,0]$

Der Graph von minus x hoch 3 plus 4 x Quadrat — Der Graph von $f(x)=-x^3+4x^2$

Lösung mit Hilfe von Umformungen

Wie eine Gleichung kann man auch eine Ungleichung mit Hilfe von Äquivalenzumformungen lösen.
Bei Ungleichungen ist zu beachten, dass sich das Relations-Zeichen bei Multiplikation mit bzw. Division durch eine negative Zahl umdreht.
Auch beim Bilden des Kehrwerts muss man das Relations-Zeichen umdrehen, wenn beide Seiten positiv oder beide negativ sind.

Lösung mit Hilfe von Logik

Manchmal lässt sich eine Ungleichung durch reine Logik lösen.
Dies ist vor allem dann möglich, wenn auf der einen Seite ein Produkt oder ein Bruch steht und auf der anderen Seite eine 0.
Bei Produkten mit mehr als zwei Faktoren wird diese Methode schnell unübersichtlich.

Beispiel 1
Löse $(x-1)\cdot(x+3) \gt 0$

Das Produkt aus $(x-1)$ und $(x+3)$ ist positiv, wenn

beide Faktoren positiv oder
beide Faktoren negativ sind

Also muss gelten: $x-1\gt 0 \wedge x+3\gt 0$ oder $x-1\lt 0 \wedge x+3\lt 0$
Damit ist entweder

$x\gt 1 \wedge x\gt -3$, also $x\gt 1$ oder
$x\lt 1 \wedge x\lt -3$, also $x\lt -3$

$\mathbb L = ]-\infty;\,-3[\;\cup\;]1;\,\infty[$

Beispiel 2
Löse $\frac{2x-3}{x+1} \lt 1 \Leftrightarrow \frac{2x-3}{x+1}-1 \lt 0 \Leftrightarrow \frac{2x-3-(x+1)}{x+1} \lt 0 \Leftrightarrow \frac{x-4}{x+1} \lt 0 $

Der Bruch ist negativ, wenn Nenner und Zähler unterschiedliche Vorzeichen haben.

Also muss gelten: $x-4\lt 0 \wedge x+1\gt 0$ oder $x-4\gt 0 \wedge x+1\lt 0$

Somit gilt

$(x\lt 4 \wedge x\gt -1) \vee (x\gt 4 \wedge x\lt -1) $
$(x\gt -1 \wedge x\lt 4) \vee f $
$x\gt -1 \wedge x\lt 4 $

$\mathbb L = ]-1;\,4[$

Aufgaben

Löse folgende Ungleichung mit Hilfe des Schaubilds.
$x^2-x\lt 0$

$f(x)=x^2-x=x(x-1)$
einfache Nullstellen: $x_1=0$, $x_2=1$ (beide mit VZW)
Verlauf von links oben nach rechts oben.
$\mathbb{L}=]0;\,1[$

Der Graph
Löse folgende Ungleichung mit Hilfe des Schaubilds.
$-x^2+x+20\geq 0$

$f(x)=-x^2+x+20$
$x_{1,2}=\dfrac{-1\pm\sqrt{1-4(-1)20}}{2(-1)}=\dfrac{-1\pm 9}{-2}$
$x_1 = -4\vee x_2=5$ sind einfache Nullstellen
Verlauf von links unten nach rechts unten.
$\mathbb{L}=[-4;\,5]$

Der Graph
Löse folgende Ungleichung mit Hilfe des Schaubilds.
$(x+3)(x+1)(x-4)\leq 0$

$f(x)=(x+3)(x+1)(x-4)$
Hat drei einfache Nullstellen: $x_1=-3, x_2=-1$ und $x_3=4$
Verlauf von links unten nach rechts oben.
$\mathbb{L}=\{x\mid x\leq -3 \vee -1\leq x\leq 4\}$ $=]-\infty;\,-3]\cup [-1;\,4]$
oder $\mathbb{L}=]-\infty;\,4]\,\setminus\; ]-3;\,-1[$

Der Graph
Löse folgende Ungleichung mit Hilfe des Schaubilds.
$(x+7)^3(x+3)(x-2)^2\leq 0$

$f(x)=(x+7)^3(x+3)(x-2)^2$ ist ein Polynom vom Grad 6.
Der Vorfaktor vor $x^6$ ist positiv, somit verläuft das Schaubild von links oben nach rechts oben.
Es hat eine dreifache Nullstelle bei $x=-7$ (VZW)
eine einfache bei $x=-3$ (VZW) und
eine doppelte bei $x=2$ (kein VZW)
$\mathbb L = [-7;\,-3]\cup\{2\}$
Löse folgende Ungleichung mit Hilfe des Schaubilds.
$-2\cdot 3^x+9\gt 0$

$f(x)=-2\cdot 3^x+9$
$\begin{array}{rcl} -2\cdot 3^x+9 &=&0\\ 3^x &=& \frac92\\ x &=& \log_3\left(\frac92\right)\\ x&\approx&1{,}36907 \end{array}$
Somit ist die Lösungsmenge $\mathbb L = \left]-\infty;\,\log_3\left(\frac92\right) \right[= \left]-\infty;\,2-\log_3\left(2\right) \right[ $

Der Graph
Löse folgende Ungleichung mit Hilfe von Umformungen.
$3x -5\gt 1$

$3x -5\gt 1 \Rightarrow 3x\gt 6 \Rightarrow x\gt 2$
$\mathbb L = ]2;\,\infty[$
Löse folgende Ungleichung mit Hilfe von Umformungen.
$\frac{2x-1}{x-1}\gt 0$ mit $x\neq 1$

$\frac{2x-1}{x-1}\gt 0 \Rightarrow $ $\left(2x-1\gt 0\right)$ für $x\gt 1$ oder $\left(2x-1\lt 0\right)$ für $x\lt 1$

Für $x\gt 1$ folgt aus $2x-1\gt 0 \Rightarrow x\gt \frac12$
Da $x\gt 1 \gt \frac12$ gilt, ist $x\gt 1$ eine Lösung.

Für $x\lt 1$ folgt aus $2x-1\lt 0 \Rightarrow x\lt \frac12$
Da $x\lt \frac12 \lt 1$ gilt, ist $x\lt \frac12$ eine Lösung.

$\mathbb L = ]-\infty;\,1/2[\;\cup\;]1;\,\infty[$
Löse folgende Ungleichung mit Hilfe von Umformungen.
$7-2x\leq 4$

$7-2x\leq 4 \Rightarrow $ $-2x\leq -3 \Rightarrow $ $x\geq \frac32 $
Löse folgende Ungleichung mit Hilfe von Umformungen.
$\frac1{x+3}\lt \frac2x$ mit $x\in\mathbb{R}\setminus\{-3;\,0\}$

$\frac1{x+3}\lt \frac2x \Rightarrow $ $x\lt 2(x+3)$ für $x\gt 0$ oder $x\lt -3$ (beide Nenner positiv oder negativ) oder
$x\gt 2(x+3)$ für $-3\lt x \lt 0$
Für $x\gt 0$ oder $x\lt -3$ folgt aus $x\lt 2(x+3) \Rightarrow -6\lt x$
Aus $x\gt 0 \wedge x\gt-6$ folgt $x\gt 0$ als Lösung.
Aus $x\lt -3 \wedge x\gt-6$ folgt $-6\lt x\lt -3$ als Lösung.

Für $-3\lt x \lt 0$ folgt aus $x\gt 2(x+3) \Rightarrow -6\gt x$
Aus $-3\lt x \lt 0 \wedge x\lt-6$ folgt keine Lösung.