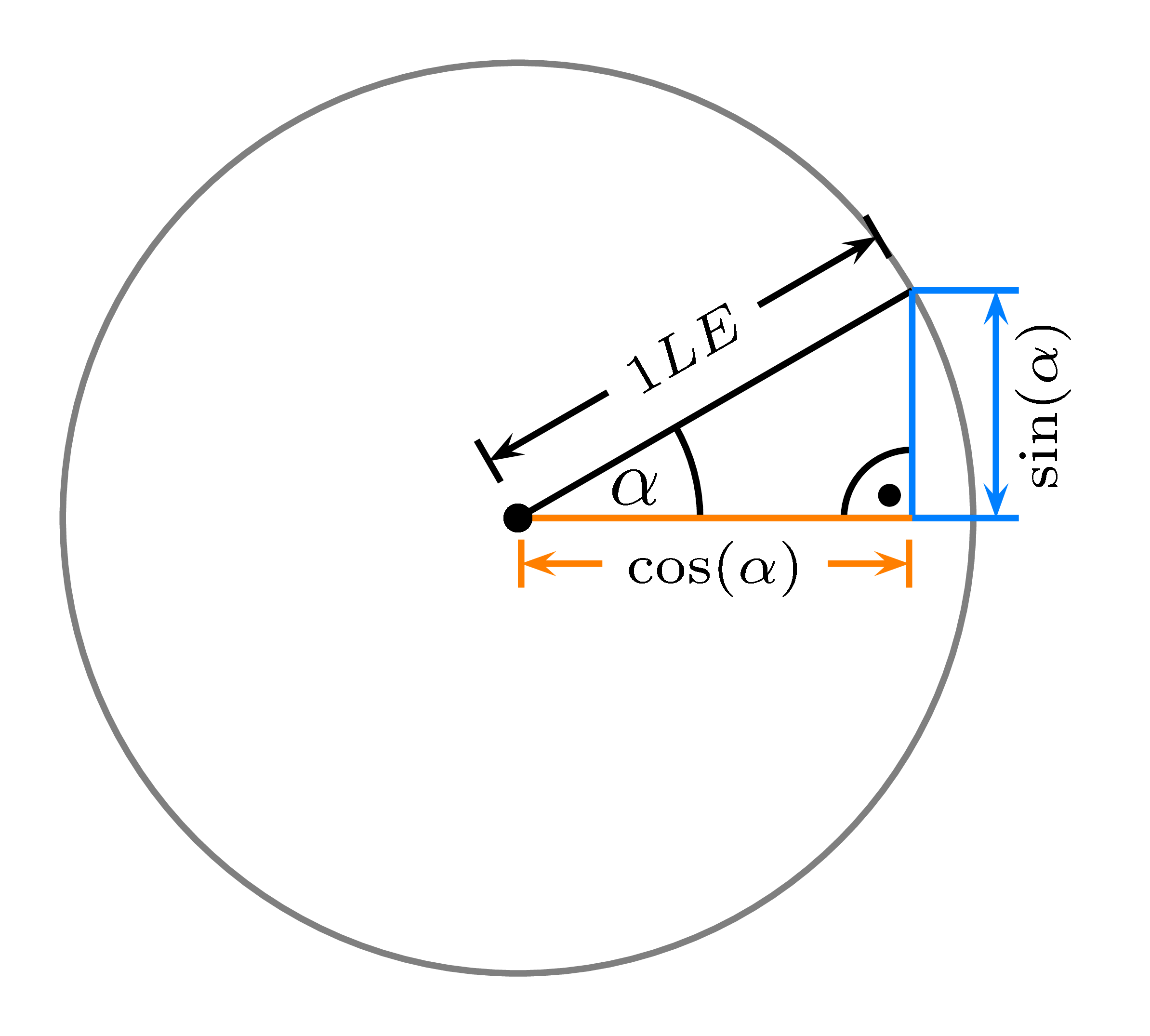
Zeichnet man im Einheitskreis einen Winkel ein und geht von dem Schnittpunkt senkrecht zur Grundlinie,
so erhält man ein rechtwinkliges Dreieck (s. Abbildung).
Da der Radius im Einheitskreis eins ist, kann man den Sinus an der Gegenkathete und den Kosinus an der Ankathete ablesen.
Da der Radius im Einheitskreis eins ist, kann man den Sinus an der Gegenkathete und den Kosinus an der Ankathete ablesen.
Mit dieser Definition von Sinus und Kosinus kann man den Definitionsbereich auf $\mathbb{R}$
erweitern.
Der Sinus von 90° oder $\frac{\pi}{2}$ ist dann 1 und der Kosinus ist 0.
Der Sinus von 180° oder $\pi$ ist dann 0 und der Kosinus ist -1.
Der Sinus von 270° oder $\frac{3\pi}2$ ist dann -1 und der Kosinus ist 0.
Der Sinus von 360° oder $2\pi$ ist dann 0 und der Kosinus ist 1.
Ab $2\pi$ wiederholen sich die Sinus- und Kosinus-Werte, somit sind sie periodisch (wiederholen sich regelmäßig).
Der Sinus von 90° oder $\frac{\pi}{2}$ ist dann 1 und der Kosinus ist 0.
Der Sinus von 180° oder $\pi$ ist dann 0 und der Kosinus ist -1.
Der Sinus von 270° oder $\frac{3\pi}2$ ist dann -1 und der Kosinus ist 0.
Der Sinus von 360° oder $2\pi$ ist dann 0 und der Kosinus ist 1.
Ab $2\pi$ wiederholen sich die Sinus- und Kosinus-Werte, somit sind sie periodisch (wiederholen sich regelmäßig).