Zeichnet man die Hilfslinien in das Schaubild ein, so sieht man:
Setzt man all dies in die allgemeine Sinus-Funktion $f(x)=a\cdot\sin(b(x-c))+d$ ein erhält man:
$f(x)=2\cdot\sin(\pi(x-0))+5$ oder
$f(x)=2\cdot\sin(\pi\,x)+5$
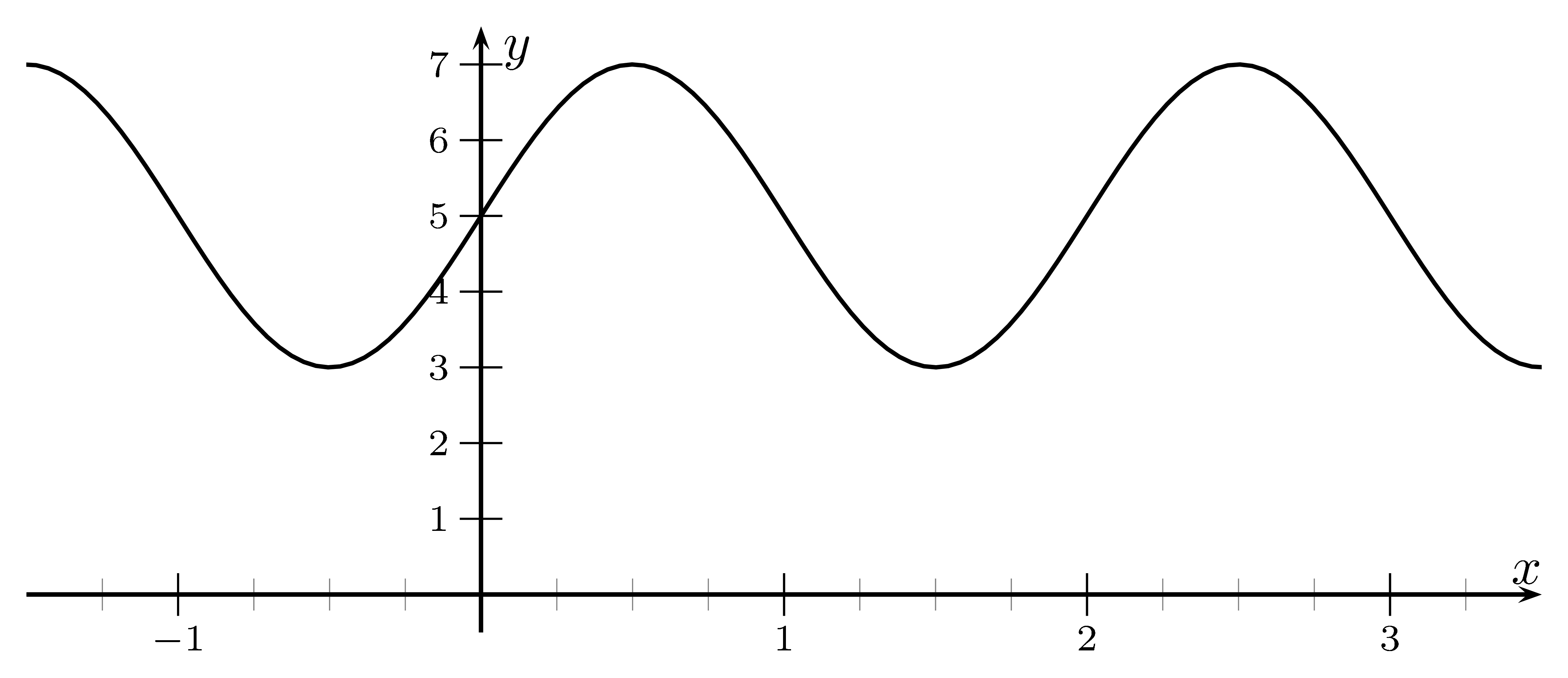
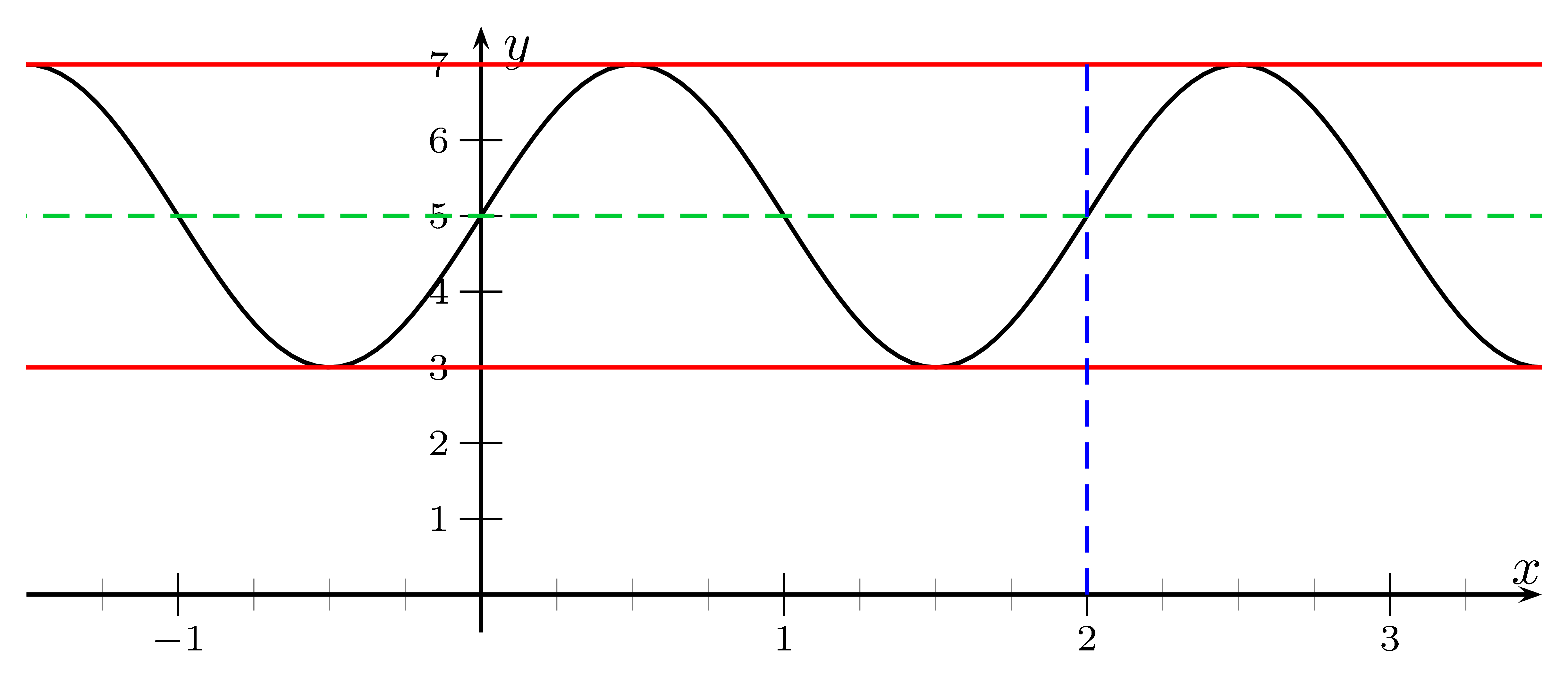
- Maximales $y=7$
- Minimales $y=3$
- Periodenlänge = 2
- Erster Schnitt von Mittellinie und Graph bei $x=0$
Die Funktion geht von $y=3$ bis $y=7$.
Damit ist die Amplitude $a= \frac{7-3}2 = \frac42 = 2$.
y-Verschiebung (d):
$d= \frac{7+3}2 = \frac{10}2 = 5$
Periodenlänge und b:
Eine Schwingung geht von $x=0$ bis $x=2$.
Die Periodenlänge ist also 2. Damit ist $b= \frac{2\pi}{2} = \pi$.
x-Verschiebung
Die Periodenlänge ist also 2. Damit ist $b= \frac{2\pi}{2} = \pi$.
Da eine Sinusfunktion gesucht ist und der erste Schnitt von Mittellinie und Graph bei
$x=0$ liegt, ist $c=0$.
Gesuchte FunktionSetzt man all dies in die allgemeine Sinus-Funktion $f(x)=a\cdot\sin(b(x-c))+d$ ein erhält man:
$f(x)=2\cdot\sin(\pi(x-0))+5$ oder
$f(x)=2\cdot\sin(\pi\,x)+5$