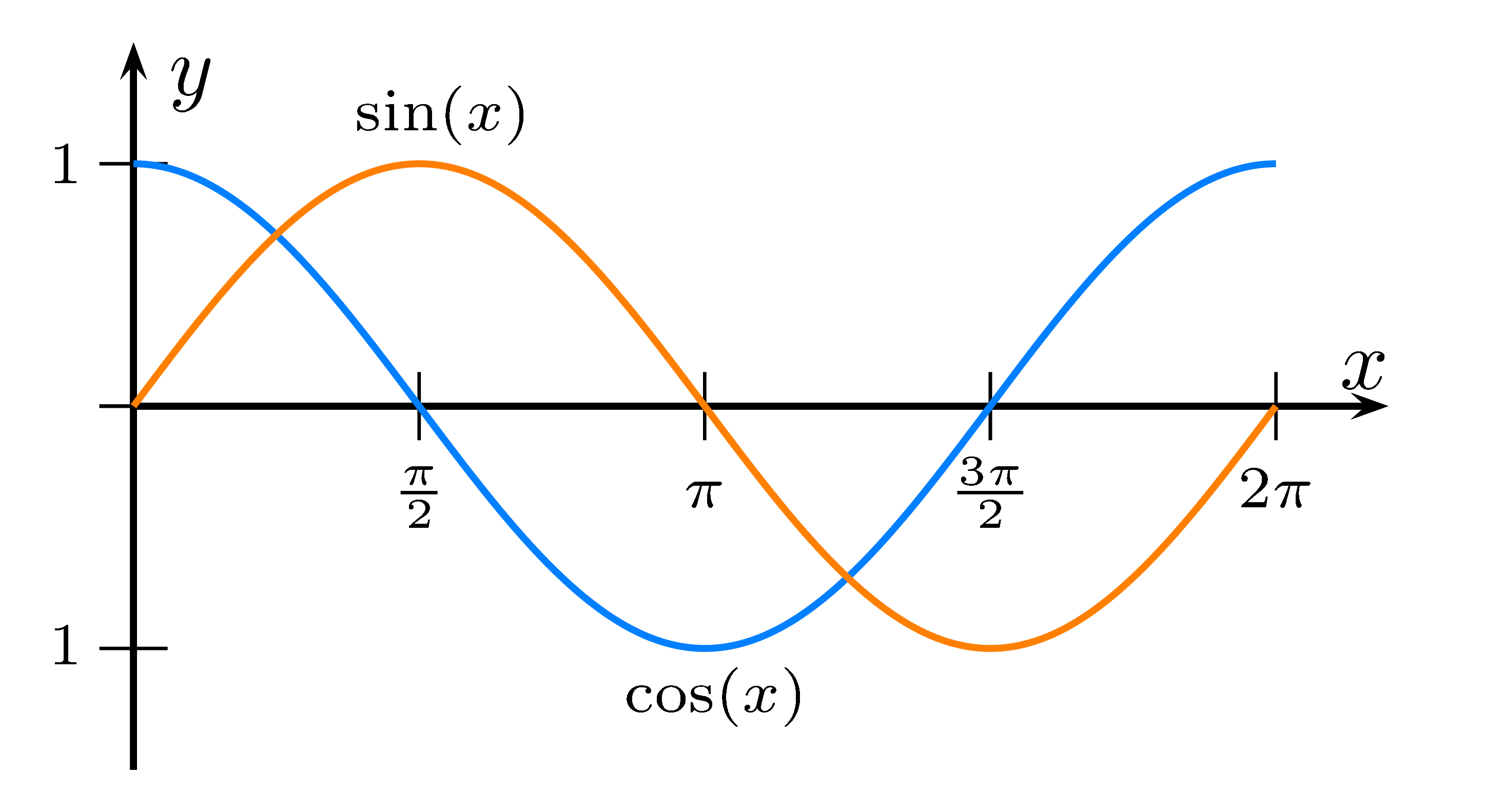
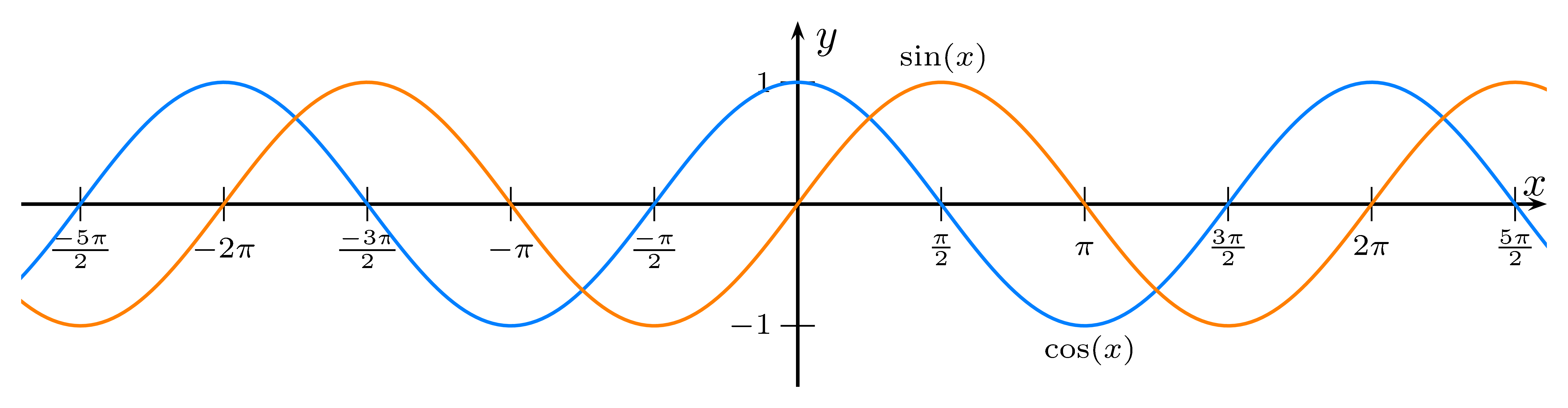
- Nullstellen:
Sinus:bei $0;\ \pi;\ 2\pi;\ 3\pi;\ 4\pi;\ 5\pi;\ \ldots$
Kosinus:bei $\frac{\pi}2;\ \frac{3\pi}2;\ \frac{5\pi}2;\ \ldots$
- Wertebereich:
$[-1;\ 1]$
Das heißt der Sinus ist immer größer oder gleich -1 und immer kleiner oder gleich 1.
Die maximale Abweichung von der Mittellinie nennt man Amplitude.
Der Sinus und Kosinus geht maximal eins über Null und maximal eins unter Null.
- Periodenlänge: Sinus und Kosinus wiederholen sich alle $2\pi$.
Somit ist $\sin(x)= \sin(x+2\pi)= \sin(x+4\pi)= \sin(x+6\pi)=\dots$
Somit ist $\cos(x)= \cos(x+2\pi)= \cos(x+4\pi)= \cos(x+6\pi)=\dots$
- Symmetrie:
Der Sinus ist ursprungssymmetrisch
Der Kosinus ist symmetrisch zur $y$-Achse
-
Besondere Sinus- und Kosinuswerte
$
\begin{array}{c|c|c|c|c|c|c|c}
\text{Grad} & 0 & 30 & 45 & 60 & 90 & 180 & 270\\\hline
\text{rad} & 0 & \frac{\pi}6 & \frac{\pi}4 & \frac{\pi}3 & \frac{\pi}2 & \pi & \frac{3\pi}6\\\hline
\sin & 0 & \frac12 & \frac{\sqrt2}2 & \frac{\sqrt3}2 & 1 & 0 & -1 \\\hline
\cos & 1 & \frac{\sqrt3}2 & \frac{\sqrt2}2 & \frac12 & 0 &-1 & 0 \\\hline
\end{array}
$
- Zusammenhang: $\cos(x)=\sin(x+\frac\pi2)$ und $\sin(x)=\cos(x-\frac\pi2)$
Der Sinus ist ein um $\frac\pi2$ verschobener Kosinus und andersherum.