Periode

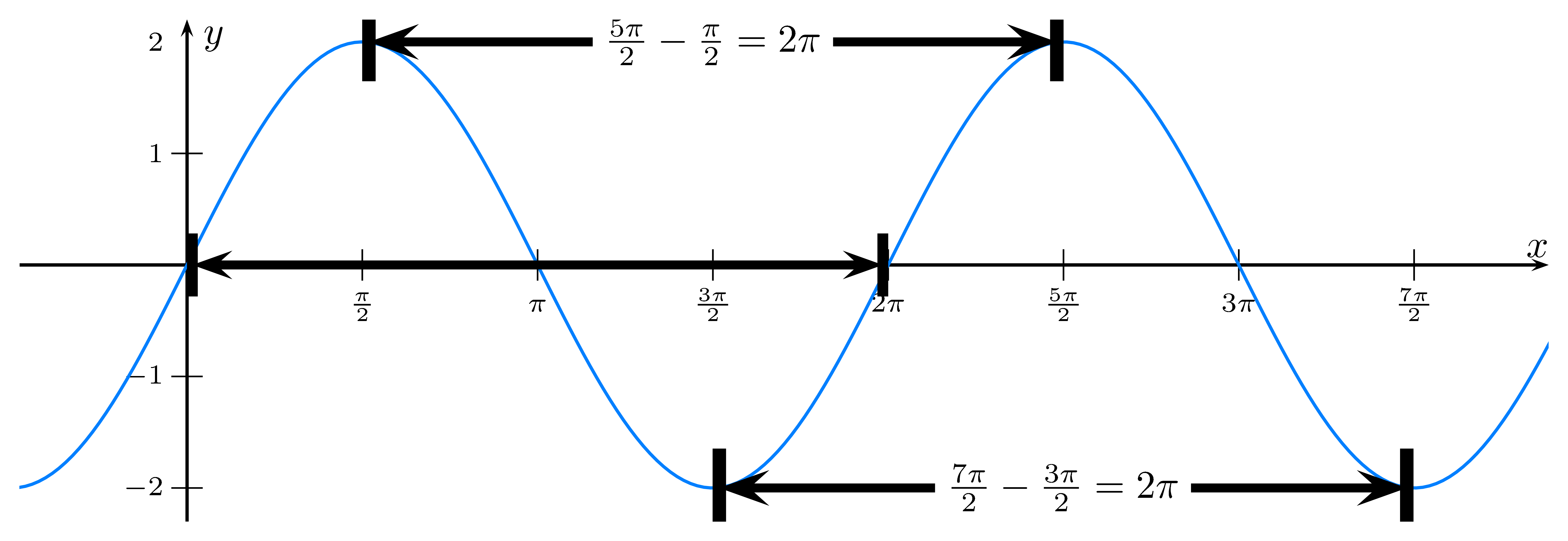
Die Periodenlänge von

$\sin(x)$ und

$\cos(x)$ ist

$2\pi$ .
Nach einer Periode wiederholt sich der Verlauf des Schaubilds.

Die ersten 3 Wiederholungen der Schaubilder von Sinus von x und Kosinus von x, also geht x von 0 bis 3 PI — Graph $\sin(x)$ und $\cos(x)$

Wird das Schaubild um den Faktor

$b$ in

$x$ -Richtung gestaucht, wird auch die Periodenlänge kleiner.

$f(x)=\sin(b\,x)$ hat eine Periodenlänge von

$\left| \frac{2\pi}b\right|$ .

$f(x)=\cos(b\,x)$ hat eine Periodenlänge von

$\left| \frac{2\pi}b\right|$ .
Die Periodenlänge hängt nur vom Vorfaktor des

$x$ im Sinus/Kosinus ab:

$f(x)=\sin(2\,x)$ hat die Periodenlänge

$\pi$ , genauso wie

$f(x)=5\sin(2\,x)$ die Periodenlänge

$\pi$ hat, genauso wie

$f(x)=\sin(2\,x-4)$ die Periodenlänge

$\pi$ hat, genauso wie

$f(x)=\sin(2\,x)+2$ die Periodenlänge

$\pi$ hat.

Periodenlänge mit dem Funktionsterm bestimmen

$f(x)=\sin(\pi\,x)$ hat die Periodenlänge $\frac{2\,\pi}{\pi}=2$
$f(x)=\cos(8\,x)$ hat die Periodenlänge $\frac{2\,\pi}{8}=\frac{\pi}{4}$
$f(x)=\cos(0{,}5\,x)$ hat die Periodenlänge $\frac{2\,\pi}{0{,}5}=4\pi$
$f(x)=\sin(-3\,x)$ hat die Periodenlänge $\frac{2\,\pi}{-3}=-\frac{2}{3}\pi$ .
Hier ist die Periodenlänge $\frac23\pi$ aber die Funktion ist zusätzlich an der $y$ -Achse gespiegelt.
Die Sinusfunktion $f(x)=\sin(b\cdot x)$ soll eine Periode der Länge 1 haben. Wie groß ist $b$ ?
$P=\frac{2\pi}{b} \Rightarrow b=\frac{2\pi}{P}$
Wenn man hier $P=1$ einsetzt bekommt man: $b=\frac{2\pi}{1}=2\pi$ .
Die Funktion $f(x)=\sin(2\pi\cdot x)$ hat also die Periodenlänge 1.

Periodenlänge vom Schaubild ablesen

Schaubild eines Sinus mit Periodenlänge 2 mal Pi — Graph einer Sinusfunktion

Der abgebildet Funktionsgraph hat eine Periodenlänge von

$2\pi$ , wie in der Abbildung ersichtlich, kann man vom Hochpunkt zum Hochpunkt, vom Tiefpunkt zum Tiefpunkt oder vom Ursprung zur übernächsten Nullstelle (wo der Graph steigt) messen und bekommt überall das selbe Ergebnis.
Der Vorfaktor vor dem

$x$ ist somit

$\frac{2\pi}{2\pi}=1$ . Hier ist noch die Amplitude eine 2, der ganze Funktionsterm ist

$2\sin(x)$

Das Schaubild der hier abgebildeten Kosinus-Funktion hat die Periodenlänge

$\pi$ und somit ist

$b=\frac{2\pi}\pi=2$ .
Man kann hier entweder vom Tiefpunkt zum Tiefpunkt messen oder vom Hochpunkt zum Tiefpunkt und dies mal 2 nehmen.

Schaubild einer Kosinus-Funktion mit Periodenlänge Pi — Graph einer Kosinus-Funktion