Das Schaubild der Funktion $f(x)$ ist
- streng monoton wachsend, wenn für jedes $x_1\lt x_2$ gilt $f(x_1)\lt f(x_2)$
- streng monoton fallend, wenn für jedes $x_1\lt x_2$ gilt $f(x_1)\gt f(x_2)$
Der Graph einer Funktion $f$ ist streng monoton wachsend, wenn $f'(x)\gt 0$ und
streng monoton fallend, wenn $f'(x)\lt 0$.
Die Umkehrung gilt allerdings nicht!
Ein Gegenbeispiel ist $f(x)=x^3$, da $f'(0)=0$ ist aber $x^3$ ist streng monoton wachsend.
streng monoton fallend, wenn $f'(x)\lt 0$.
Die Umkehrung gilt allerdings nicht!
Ein Gegenbeispiel ist $f(x)=x^3$, da $f'(0)=0$ ist aber $x^3$ ist streng monoton wachsend.
Anstatt Monotonie für den ganzen Definitionsbereich zu überprüfen, kann man sie auch auf Intervallen testen.
Der Graph von $f(x)=x^2$ ist streng monoton fallend für $x\in]-\infty;\; 0]$ und streng monoton steigend für $x\in[0;\;\infty[$
Der Graph von $f(x)=x^2$ ist streng monoton fallend für $x\in]-\infty;\; 0]$ und streng monoton steigend für $x\in[0;\;\infty[$
Um alle Intervalle zu finden, in denen eine Funktion streng monoton fällt/wächst kann man als erstes die
Nullstellen der ersten Ableitung $f'(x)$ bestimmen.
Bei stetigen Ableitungsfunktionen kann sich das Vorzeichen der Ableitung ja nur an den Nullstellen ändern (d.h. nur hier kann der Graph der Funktion von wachsend auf fallend (oder andersherum) übergehen).
Um zu Überprüfen, ob $f(x)$ zwischen zwei Nullstellen von $f'(x)$ wächst oder fällt, setzt man einfach einen $x$-Wert zwischen den Nullstellen in $f'(x)$ ein. Ist $f'(x)\gt 0 $ wächst der Graph und ist $f'(x)\lt 0$ fällt er.
Bei stetigen Ableitungsfunktionen kann sich das Vorzeichen der Ableitung ja nur an den Nullstellen ändern (d.h. nur hier kann der Graph der Funktion von wachsend auf fallend (oder andersherum) übergehen).
Um zu Überprüfen, ob $f(x)$ zwischen zwei Nullstellen von $f'(x)$ wächst oder fällt, setzt man einfach einen $x$-Wert zwischen den Nullstellen in $f'(x)$ ein. Ist $f'(x)\gt 0 $ wächst der Graph und ist $f'(x)\lt 0$ fällt er.
Beispiel:
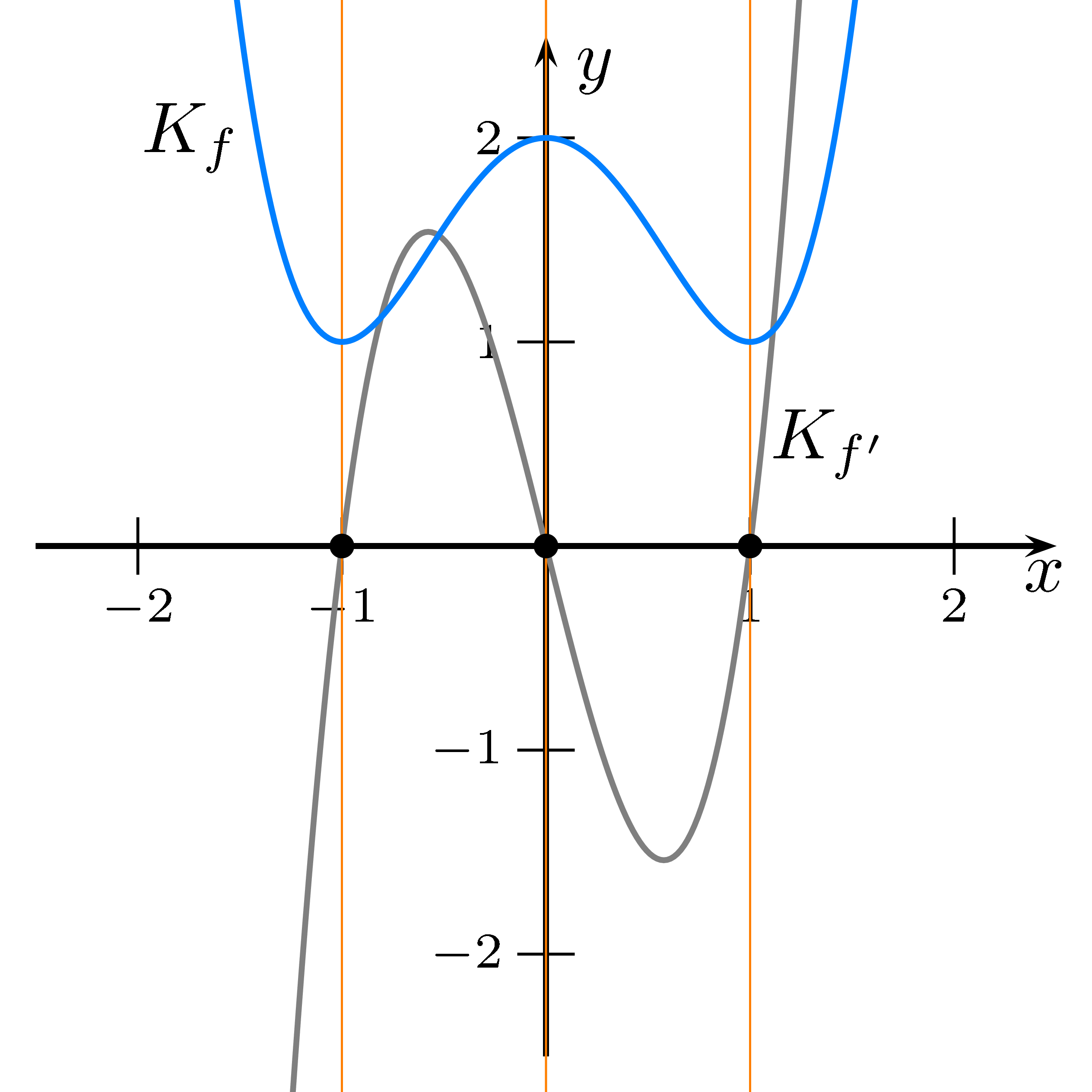
Gegeben: Funktion $f(x)=x^4-2x^2+2$. Ihr Schaubild heißt $K_f$.
Gesucht: Die Intervalle in welchen $f(x)$ streng monoton steigt bzw. fällt. Lösung:
Gegeben: Funktion $f(x)=x^4-2x^2+2$. Ihr Schaubild heißt $K_f$.
Gesucht: Die Intervalle in welchen $f(x)$ streng monoton steigt bzw. fällt. Lösung:
- Ableitung bestimmen: $f'(x)=4x^3-4x$
- Nullstellen der Ableitung: $f'(x)=0$
Man erhält: $x_0=-1$, $x_1=0$ und $x_2=1$ -
Für $x\lt -1$ ist die Ableitung kleiner als 0 (z.B. $f'(-2)=-24\lt 0$).
Somit ist $K_f$ im Intervall $]-\infty;\;-1]$ streng monoton fallend.Für $x\in [-1;\;0]$ ist die Ableitung größer als 0
(z.B. $f'(-0{,}5)=1{,}5\gt 0$).
Somit ist $K_f$ im Intervall $[-1;\;0]$ streng monoton wachsend.Für $x \in [0;\;1]$ ist die Ableitung kleiner als 0 (z.B. $f'(0{,}5)=-1{,}5\lt 0$).Für $x\gt 1$ ist die Ableitung größer als 0 (z.B. $f'(2)=24\gt 0$).
Somit ist $K_f$ im Intervall $[0;\;1]$ streng monoton fallend.
Somit ist $K_f$ im Intervall $[1;\;\infty[$ streng monoton wachsend.