Impressum
< Index

Bestimmtes Integral

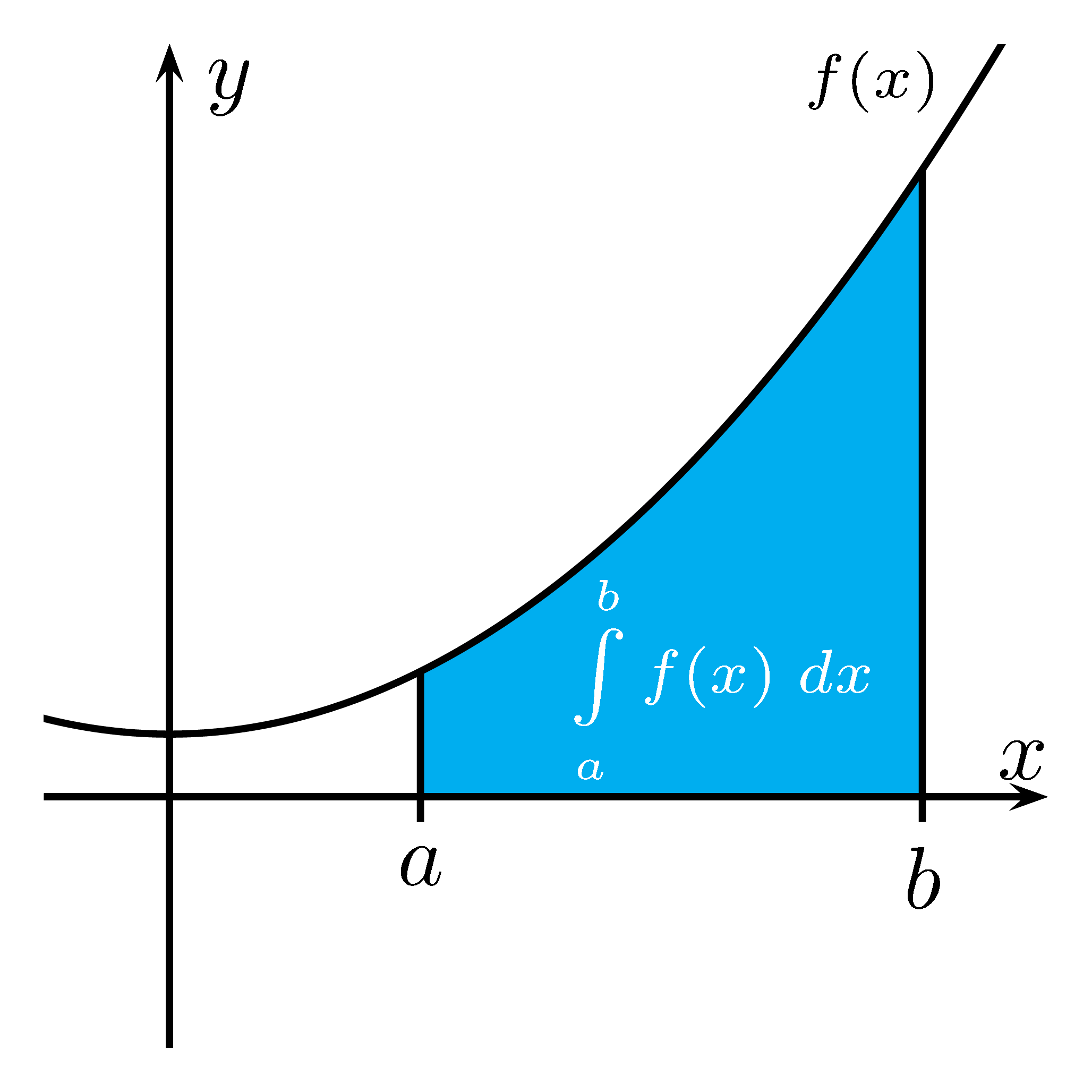
Das bestimmte Integral $\int\limits_a^b f(x)\;dx$ gibt die Fläche zwischen der Kurve und der $x$-Achse für das Intervall $[a;\; b]$ an.
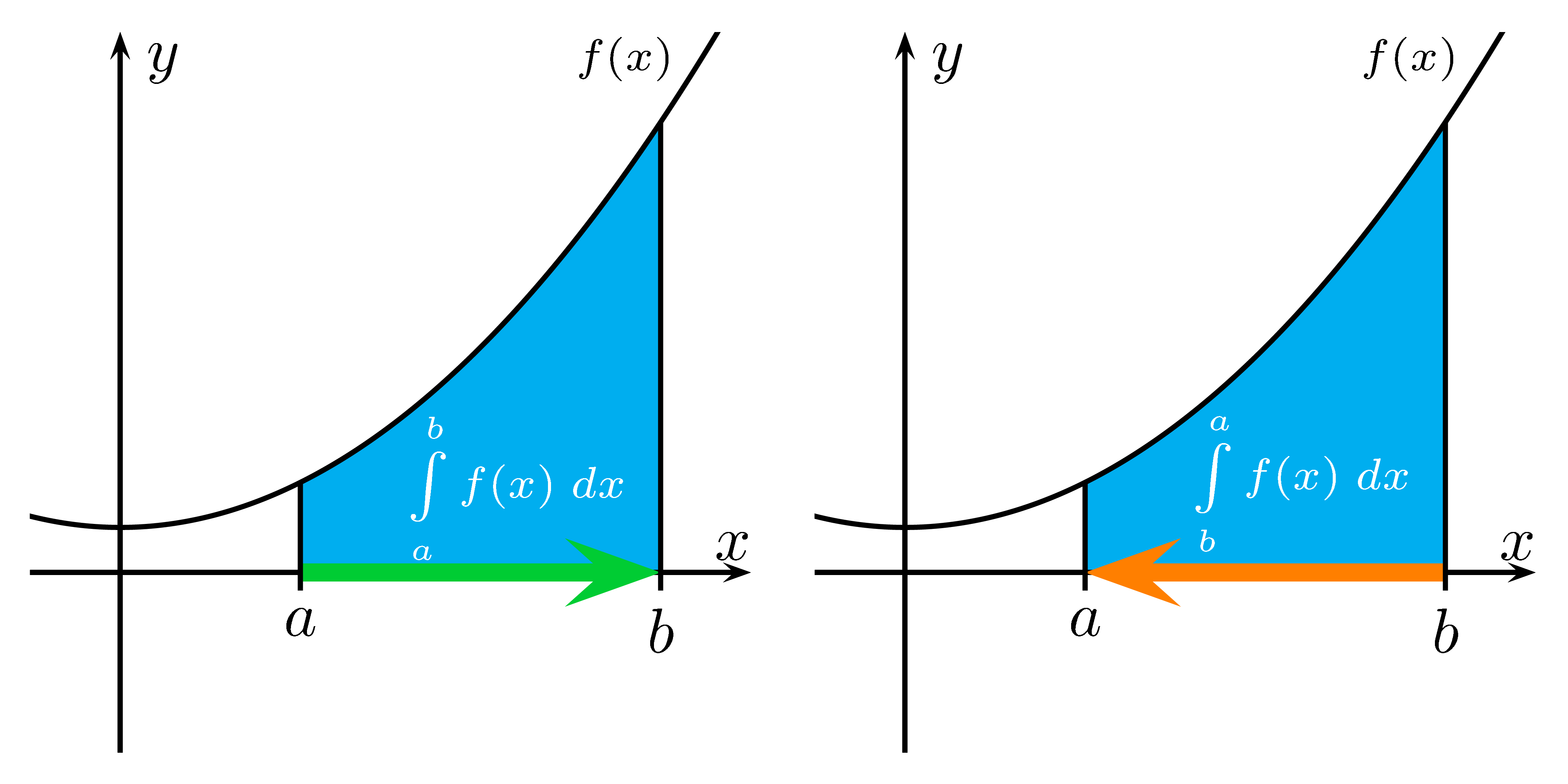
Hierbei haben Flächen unter der $x$-Achse einen negativen Wert und Fläche oberhalb eine positiven.
Das bestimmte Integral $\int\limits_a^b f(x)\;dx$ und die Stammfunktion $F(x)=\int f(x)\;dx$ hängen wie folgt zusammen: $$\int\limits_a^b f(x)\;dx = F(b)-F(a)$$ Das heißt die Fläche unter dem Graph von $f(x)$ in dem Bereich $a\leq x \leq b$ ist so groß wie die Stammfunktion an der Stelle $b$ minus die Stammfunktion an der Stelle $a$.
Für $F(b)-F(a)$ schreibt man abkürzend auch $[F(x)]_a^b$ oder $F(x)\Big|_a^b$.
Funktion f mit einer blauen Fläche unter f von a bis b
Das bestimme Integral ist die Fläche zwischen Kurve und $x$-Achse.
Regeln
• $\int\limits_a^b f(x)\;dx = F(b)-F(a)$
  Das ist der Hauptsatz der Integralrechnung.
• $\int\limits_a^b f(x)\;dx = -\int\limits_b^a f(x)\;dx $
  Wenn man die Integrations-Grenzen vertauscht, ändert sich das Vorzeichen des Integrals.
Integral von a nach b und b nach a
Integral von $b$ nach $a$ und von $b$ nach $a$
• $\int\limits_a^a f(x)\;dx =0$
  Die Fläche ist 0 breit ($a-a=0$), somit ist das Integral auch 0.
• $\int\limits_a^c f(x)\;dx +\int\limits_c^b f(x)\;dx =\int\limits_a^b f(x)\;dx$
  Die Summe von aneinanderhängenden Teilflächen ist gleich groß wie die Gesamtfläche.
Das Integral von a nach c und von c nach b ist das selbe wie von a nach b
Das Integral von $a$ nach $c$ plus die von $c$ nach $b$ ist das selbe wie von $a$ nach $b$

Beispiele:

  1. Berechne: $\int\limits_1^3 x^2\; dx$
    Lösung:
    $F(x)= \int x^2\; dx = \frac13x^3+c$
    $\int\limits_1^3 x^2\; dx = \frac13x^3+c\Big|_1^3 = (\frac133^3+c)-(\frac131^3+c)= \frac{26}3 \approx 8{,}67$
  2. Berechne: $\int\limits_{-1}^1 3x^2-3\; dx$
    Lösung:
    $F(x)= \int 3x^2-3\; dx = x^3-3x+c$
    $\int\limits_{-1}^1 3x^2-3\; dx = x^3-3x+c\Big|_1^3 = (1^3-3\cdot 1+c)-((-1)^3-3\cdot(-1)x+c)= -4$
    Die Fläche ist $4FE$ groß und komplett unter der $x$-Achse, daher ist das Integral negativ.
  3. Berechne: $\int\limits_{-10}^0 e^x\; dx$
    Lösung:
    $F(x)= \int e^x\; dx = e^x+c$
    $\int\limits_{-10}^0 e^x\; dx = e^x+c\Big|_{-10}^0 = e^{0}+c- (e^{-10}+c)= 1-e^{-10} \approx 1$
  4. Aufgabe: Bestimme die Fläche zwischen der $x$-Achse und dem Graph von $\sin(x)$ in der ersten Periode überhalb der $x$-Achse.
    Lösung:
    Der Sinus verläuft von 0 bis $\pi$ über der $x$-Achse.
    Gesucht ist somit: $\int\limits_{0}^{\pi} \sin(x)\; dx$ $F(x)= \int \sin(x)\; dx = -\cos(x)+c$
    $\int\limits_0^{\pi} \sin(x)\; dx = -\cos(x)+c\Big|_0^{\pi} = -\cos(\pi)+c-(-\cos(0)+c)= 1+c-(-1+c) = 2$
    Die erste Periode des Sinus schließt im ersten Quadranten eine Fläche von $2FE$ mit der $x$-Achse ein.