Indiana Lineman

Aufgabe 1

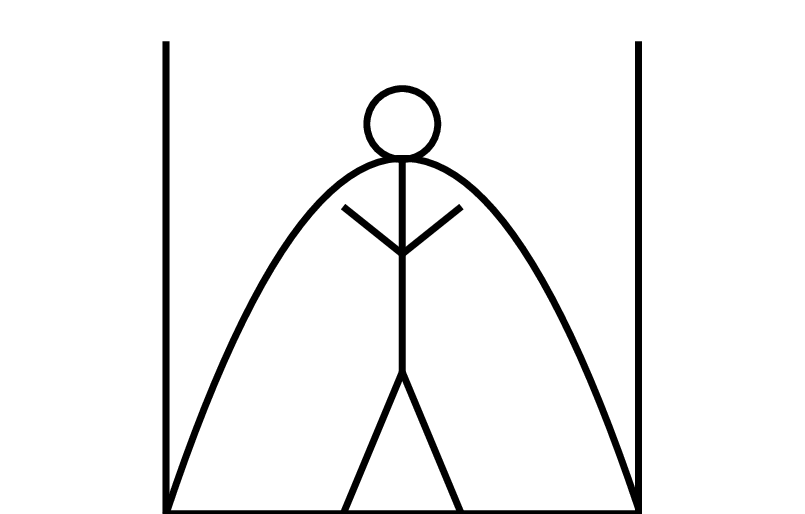
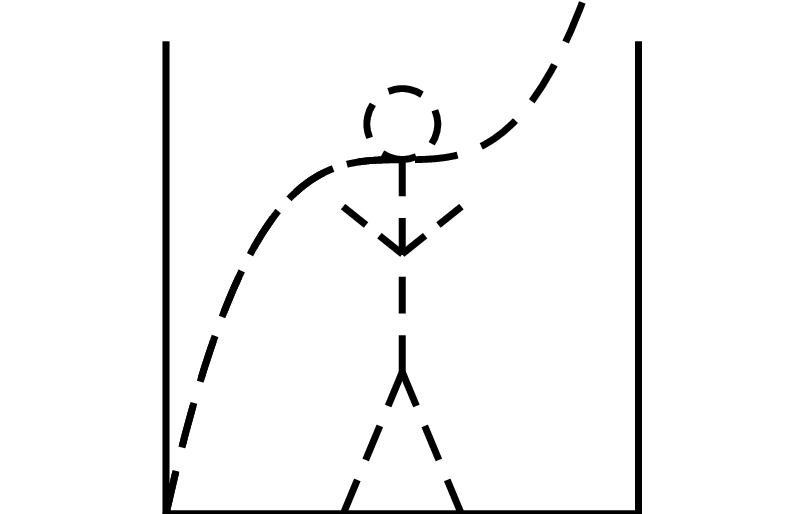
Indiana Lineman ist in einem Inkatempel in eine Fallengrube gefallen, in welche plötzlich Wasser einfließt.
Indiana ist 180cm groß und sein Hals beginnt bei 150cm.
Der Wasserstand ist durch die Funktion $$w(x) = -\frac{1}{6}x^2+10x$$ gegeben ($w(x)$ ist in cm und $x$ in Minuten angegeben).

Wann steht das Wasser 100cm hoch?
Wann steht am meisten Wasser in der Falle?
Überlebt Indiana Lineman?
Wie schnell (in cm/min) fließt das Wasser zu Beginn in die Grube?
Wann steigt das Wasser nur noch um einen cm/min?

Strichmännchen in der Grube — Indiana Lineman in der Fallgrube

Lösung

Wann steht das Wasser 100cm hoch?
Ansatz: $w(x)=100$
$\begin{array}{rcl} -\frac{1}{6}x^2+10x &=&100\\ -\frac{1}{6}x^2+10x-100 &=&0\\ \end{array}$

$x_{1,2}=\dfrac{-10\pm \sqrt{10^2-4\left(-\frac16\right)(-100)}}{2\left(-\frac16\right)}$
$x_{1,2}=\dfrac{-10\pm \sqrt{\frac{100}3}}{-\frac13}$

$x_1 = 12{,}68$
$x_2 = 47{,}32$
Nach 12,68min und nach 47,32min steht das Wasser 100cm hoch.
Wann steht am meisten Wasser in der Falle? Überlebt Indiana Lineman?
Ansatz: $w'(x)=0$
$w'(x)= -\frac13x+10$
$\begin{array}{rcl} -\frac13x+10 &=&0\\ x &=&30\\ \end{array}$
Nach 30min steigt das Wasser nicht mehr.
Der Wasserstand ist dann $w(30)=-\frac16\cdot30^2+10\cdot30 = 150$cm.
Somit überlebt Indiana Lineman.
Wie schnell (in cm/min) fließt das Wasser zu Beginn in die Grube?
Ansatz: $w'(0)$ ist die Änderungsrate des Wasserstands nach 0min.
$w'(0) = -\frac13\cdot0+10$
Das Wasser steigt zu Beginn mit 10cm/min.
Wann steigt das Wasser nur noch um einen cm/min?
Ansatz: $w'(0)=1$
$\begin{array}{rcl} -\frac13x+10 &=& 1 \\ -\frac13x &=& -9 \\ x &=& 27 \\ \end{array}$
Nach 27min steigt das Wasser nur noch mit einem cm pro Minute.

Strichmännchen in der Grube mit Wasserstandskurve — Indiana Lineman mit Wasserstandskurve

Aufgabe 2

Corny Dashman ist in einem anderen Inkatempel ebenfalls in eine Fallengrube gefallen, in welche plötzlich Wasser einfließt. Auch Corny ist 180cm groß und sein Hals beginnt bei 150cm. Der Wasserstand ist dieser Fallgrube ist durch die Funktion $$h(x) = \frac {1}{180}x^3-\frac {1}{2}x^2+15x$$.

Wann steigt der Wasserspiegel nicht?
Ist dies der höchste Wasserstand?
Wann steigt der Wasserspiegel um 2cm/min?
Überlebt Corny Dashman?

Dashman in der Grube — Corny Dashman in der Fallgrube

Lösung

Wann steigt der Wasserspiegel nicht? Ist dies der höchste Wasserstand? Ansatz: $h'(x)=0$ mit $h'(x)=\frac{1}{60}x^2-x+15$
$\frac{1}{60}x^2-x+15=0$
$x_{1,2}=\dfrac{1\pm\sqrt{(-1)^2-4\cdot\frac{1}{60}\cdot15}}{2\cdot \frac1{60}}$
$x_{1,2}=\dfrac{1\pm\sqrt{0}}{\frac1{30}}=30$
Nach 30min steigt das Wasser nicht mehr (bei einer Höhe von $h(30)=150$).
Allerdings steigt danach der Wasserstand weiter, es ist somit nicht der höchste Wasserstand.
z.B. ist $h(45)=168{,}75$cm
Wann steigt der Wasserspiegel um 2cm/min?
Ansatz: $h'(x)=2$
$\frac{1}{60}x^2-x+15=2$
also $\frac{1}{60}x^2-x+13=0$
$x_{1,2}=\dfrac{1\pm{1-4\cdot\frac{1}{60}\cdot13}}{2\cdot\frac{1}{60}}$ $x_{1,2}=\dfrac{1\pm{\frac{2}{15}}}{\frac{1}{30}}$ $x_1 = 19{,}05$ und $x_2=40{,}95$
Bei 19,05min und 40,95min steigt das Wasser mit 2cm/min.
Überlebt Corny Dashman? - Nein, er ertrinkt. Mit gestrichelten Armen kann man nämlich nicht schwimmen.