Aufgaben f'

Aufgaben zur ersten Ableitung (Tangenten, Normale)

Aufgabe 1 - Steigung, Tangenten, Normalen

Gegeben ist die Funktion $f$ mit $f(x)=2x-\frac 1 4 x^2$; $x\in \mathbb{R}$.
$K_f$ ist das Schaubild von $f$.

Bestimmen Sie die Steigung von $K$ an der Stelle $x_0$ mit $x_0 \in \{-4;-1;0;1{,}5;3\}$.
In welchem Punkt hat $K$ eine Tangente mit der Steigung 3?
Bestimmen Sie die Gleichung der Tangente an $K$ in $P(2|f(2))$.
Wie lautet die Gleichung der Normalen in $P$?
Zeichnen Sie $K$, Tangente und Normale in ein Koordinatensystem.
$K_g$ ist das Schaubild der Funktion $g$ mit $g(x)=t\cdot f(x)$; $t\in\mathbb{R}^*$ (also $t\gt 0$).
$K_g$ schneidet die $X$-Achse in $S_1$ und $S_2$.
Für welche Werte von $t$ sind die Tangenten in $S_1$ und $S_2$ orthogonal zueinander?

Lösungen

$f'(x)=2-\frac 1 2 x$
$\begin{array}{l|rrrrr} x & -4 & -1 & 0 & 1{,}5 & 3\\\hline f'(x) & 4 &\frac 5 2 & 2 & \frac 5 4 & \frac 1 2\\ \end{array}$
$f'(x)=3$
$2-\frac12x =3$
$-\frac12x =1$
$ x =-2$
$f(-2)=-5$
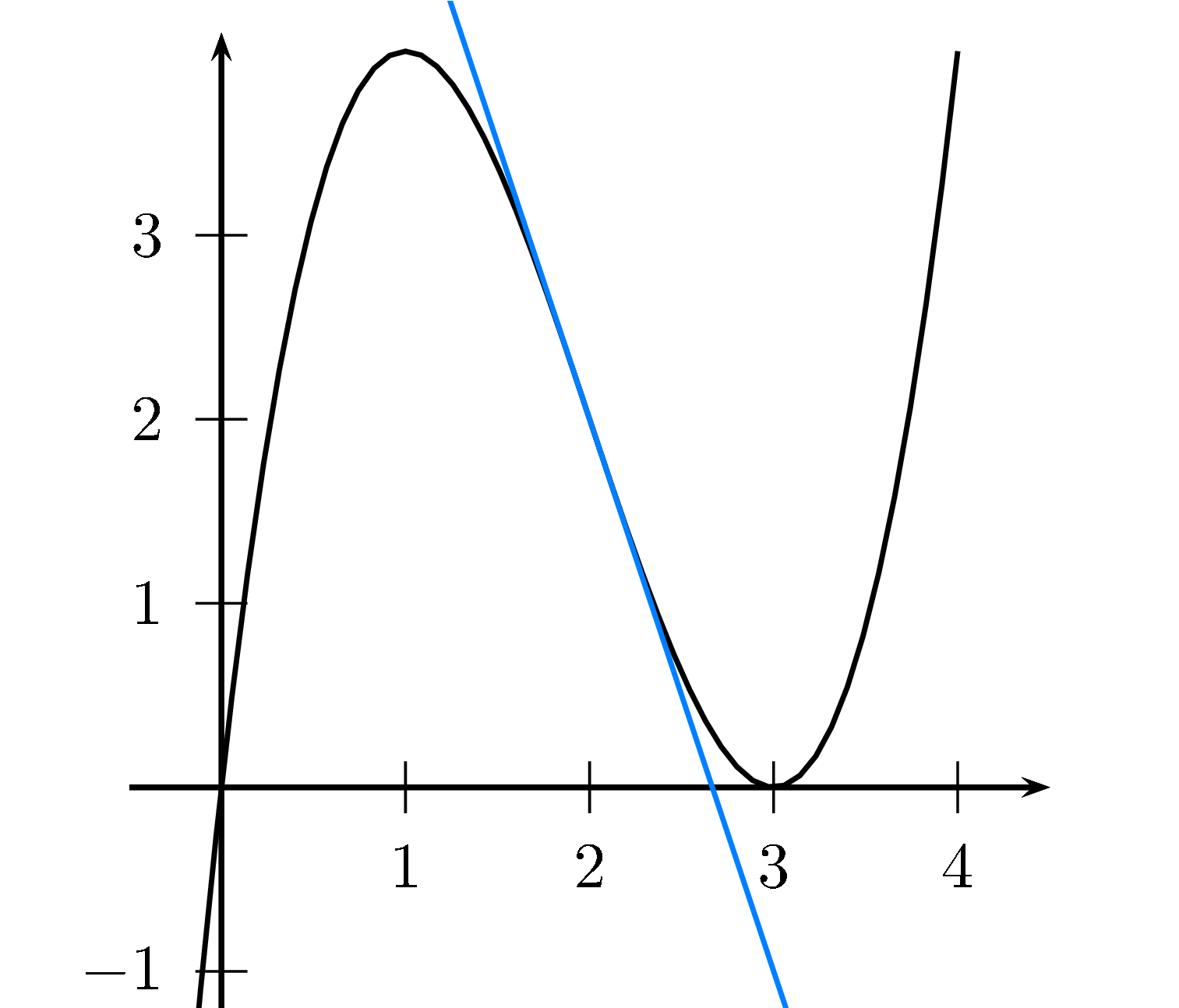
$P(-2\mid -5)$
geg. $P(2\mid 3)$ und $f'(x)=2-\frac12x$
$m=f'(2)=1$
$P$ und $m$ in $y=mx+b$ einsetzen und man erhält die Tangentengleichung: $y=x+1$
Die Normale hat die Steigung $m_2=-\frac{1}{f'(2)}=-1$
Setzt man $m_2$ und $P$ in die Gleichung $y=mx+b$ ein erhält man die Normalengleichung: $y=-x+5$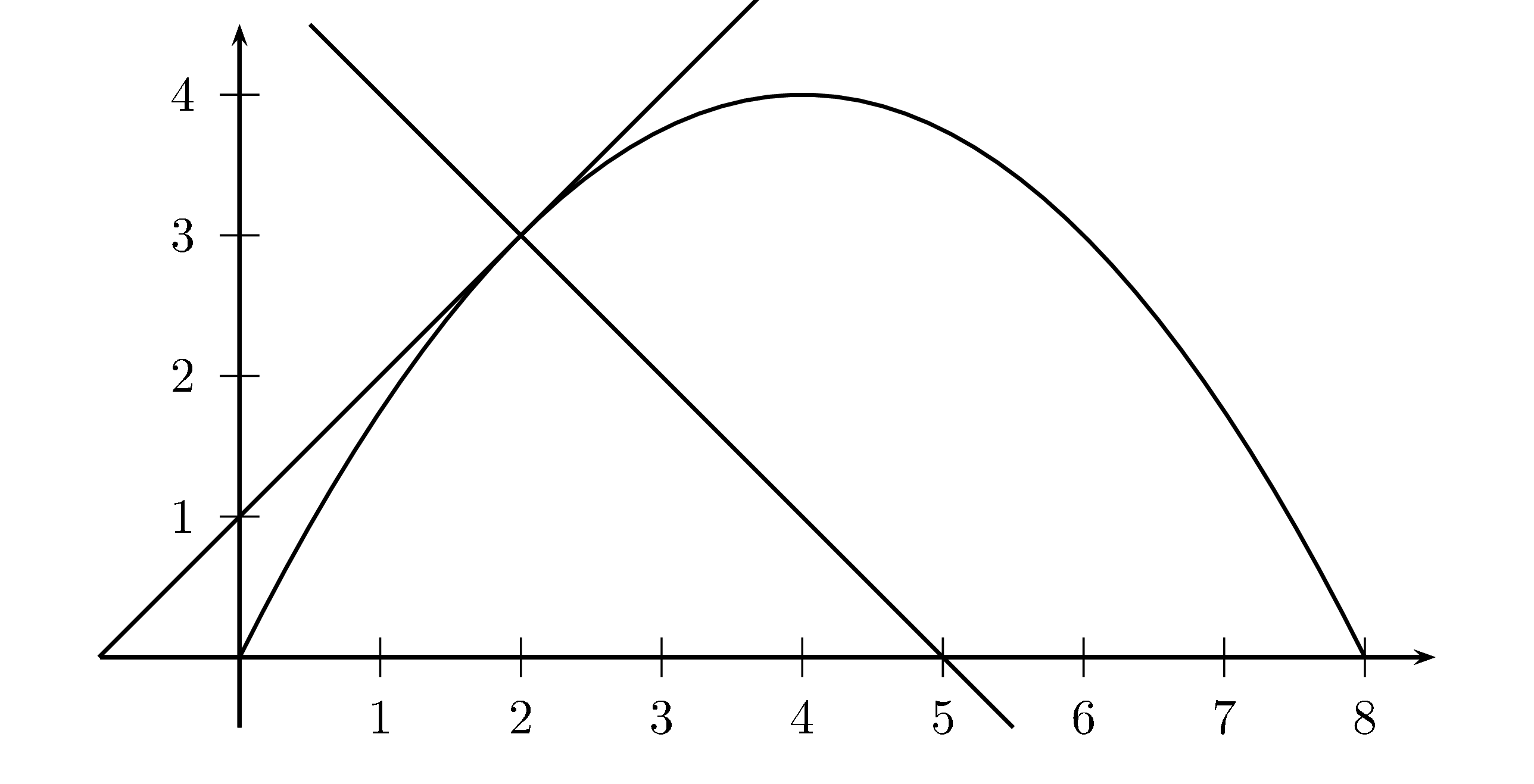

Das Schaubild $K_f$ mit der Tangente und Normale in $P(2\mid 3)$
$g(x)=t\cdot f(x)=t(2x-\frac 1 4 x^2)$
Die Nullstellen erhält man über den Satz vom Nullprodukt.
$0=t\cdot x\cdot (2-\frac14 x)$
Somit sind $S_1(0\mid 0) und S_2(8\mid 0)$ die Schnittpunkte von $K_g$ mit der $X$-Achse.
Da sich die Tangenten in $S_1$ und $S_2$ senkrecht schneiden sollen gilt:
$g'(0)\cdot g'(8)=-1$
$(2t-\frac{t}2\cdot0)(2t-\frac{t}{2}\cdot 8)=-1$
$(2t)(2t-4t)=-1$
$(2t)(-2t)=-1$
$-4t^2=-1$
$t = \pm \frac12$
Da $t\gt 0$ sein muss (laut Aufgabenstellung), ist die einzige Lösung $t=\frac12$
Somit hat $g(x)=\frac12\cdot f(x)= \frac12(2x-\frac 1 4 x^2) = x-\frac18x^2$ in den Nullstellen Tangenten, die sich senkrecht schneiden.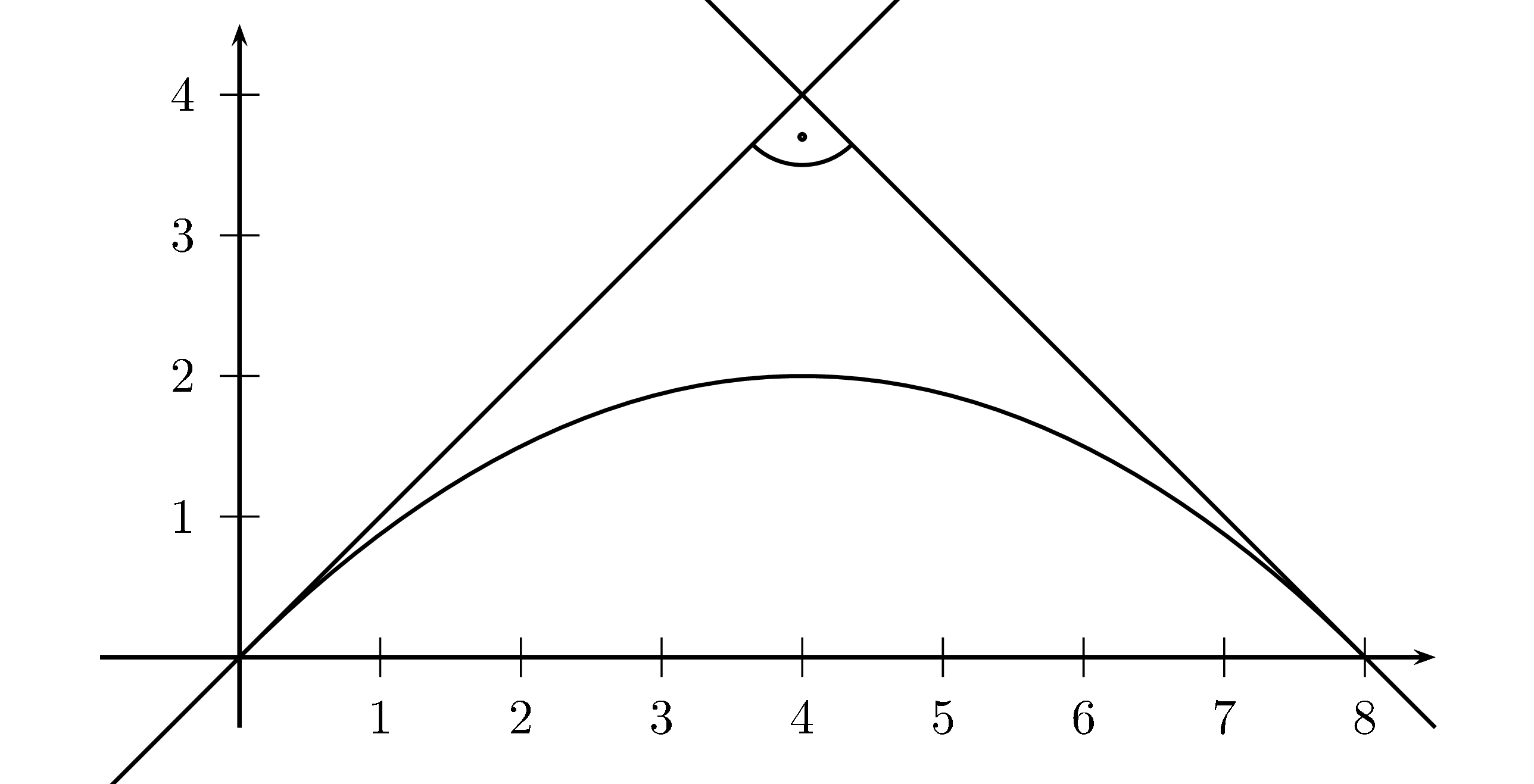

Das Schaubild $K_g$ mit den zwei Tangenten

Aufgabe 2 - Steigung, Symmetrie und Tangenten

Gegeben ist die Funktion $f$ mit $f(x)=\frac 1 9 x^3-x$; $x\in\mathbb{R}$.
$K$ ist das Schaubild von $f$.

An welchen Stellen hat $K$ die Steigung 2?
Die Steigung von $K$ an der Stelle $x=1{,}5$ ist $-0{,}25$.
Geben Sie ohne Rechnung eine weitere Stelle mit der gleichen Steigung an.
Begründen Sie ihre Vermutung.
In welchen Kurvenpunkten hat $K$ eine waagerechte Tangente?
Geben Sie die Gleichung an.
Bestimmen Sie die Gleichung der Tangente an $K$ im Ursprung.
Bestimmen Sie die Gleichung der Tangente an $K$ im Punkt $P(u\mid f(u))$.
Welche Gerade schneidet $K$ in $N(3\mid 0)$ senkrecht?

Lösungen

$f'(x)=\frac 1 3 x^2-1$
Ansatz: $f'(x)=2$ liefert $x_{1,2}=\pm3$
$K$ ist symmetrisch zum Ursprung, da es nur ungerade Potenzen hat.
Wegen dieser Symmetrie zum Ursprung gilt: $f'(1{,}5)=f'(-1{,}5)=-0{,}25$
Ansatz: $f'(x)=0$ liefert $x_{1,2}=\pm\sqrt3$
Die $y$-Werte sind:
$f\left(\sqrt3\right) = -\frac 2 3\sqrt 3$ und
$f\left(-\sqrt3\right) = \frac 2 3\sqrt 3$ und

Da die Steigung 0 ist, sind die Tangenten waagerecht:
$y_1=-\frac 2 3 \sqrt 3$
$y_2= \frac 2 3 \sqrt 3$
Im Urspurng $(0\mid 0)$ ist die Steigung $m=f'(0)=-1$.
Die Tangente ist also eine Ursprungsgerade mit Steigung -1: $y=-x$
Die Steigung im Punkt $P(u\mid f(u))$ ist $f'(u)=\frac 1 3 u^2-1$.
Und $f(u)= \frac 1 9 u^3-u$.
Setzt man den Punkt und die Steigung in die PSF ein oder in $y=mx+b$, erhält man

$\frac 1 9 u^3-u = \left(\frac 1 3 u^2-1\right)u+b$
$\frac 1 9 u^3-u = \frac 1 3 u^3-u+b$
$b = -\frac 1 3 u^3+u +\frac 1 9 u^3-u$
$b = -\frac 2 9 u^3$

Gleichung der Tangente in $P\left(u\mid \frac 1 9 u^3-u\right)$: $y=\left(\frac 1 3 u^2-1\right)x-\frac 2 9 u^3$
Gegeben ist der Punkt $N(3\mid 0)$ und mit der Ableitung bekommt man die Steigung in $N$.
$f'(3)=2$
Die Senkrechte hat also die Steigung: $m=-\frac12$
Stellt man mit $m$ und $N$ die Geradengleichung auf erhält man: $y=-\frac 1 2 x +\frac 3 2$

Aufgabe 3 - Tangenten und Symmetrie

Gegeben ist die Funktion $f$ mit $f(x)=\frac{x^4}{4}-\frac 3 4 x^2 -1$; $x\in\mathbb R$.
$K$ ist das Schaubild von $f$.

Bestimmen Sie die Nullstellen und Extrema von $K$ und geben Sie die zugehörigen Steigungen an.
Die Tangenten an $K$ in $x=1$ und $x=-1$ schneiden sich auf der $Y$-Achse.
Begründen Sie diese Behauptung.

Lösungen

$N_{1,2}(\pm 2|0)$ mit $f'(\pm2)=\pm 5$
$E_1(0|-1)$ mit $f'(0)=0$
$E_{2,3}\left(\pm\sqrt{1{,}5}|-\frac{25}{16}\right)$ mit $f'\left(\pm\sqrt{1{,}5}\right)=0$
Da $K$ symmetrisch zur $y$-Achse ist, sind $f(-1)=f(1)$.
Die Ableitung ist symmetrisch zum Ursprung, somit gilt $f'(-1)=-f'(1)$.
Somit ist $P_1(-1\mid f(-1))$ und $P_2(1\mid f(1))$ gleich weit von der $y$-Achse entfernt.
Da die Steigungen nur ein unterschiedliches Vorzeichen haben, treffen sie sich auf der $y$-Achse.
Einfacher ausgedrückt, da $K$ symmetrisch zur $y$-Achse ist muss auch die Tangente bei -1 das Spiegelbild von der bei 1 sein.

Für Leute die dies Nachrechnen wollen:
Tangente in $x_1=1:\qquad y=-\frac 1 2x-1$
Tangente in $x_2=-1:\qquad y=\frac 1 2x-1$
$S(0|-1)$ auf der $y$-Achse, da $K$ symmetrisch zur $Y$-Achse ist.

Aufgabe 4 - Tangenten und Symmetrie

Gegeben ist die Funktion $f$ mit $f(x)=-x^4+2x^3$; $x\in\mathbb R$. $K$ ist das Schaubild von $f$.

Untersuchen Sie $K$ auf Schnittpunkte mit der $x$-Achse und Punkte mit waagerechter Tangente.
$g$ ist die Tangente an $K$ in $P(1|f(1))$. Bestimmen Sie die Gleichung der Tangente.
Zeigen Sie, dass $K$ bei $x=2$ eine Normale mit Steigung $\frac 1 8$ hat.
Geben Sie die Gleichung der Normalen an.

Lösungen

Nullstellen
$f(x)=0$
$0=-x^4+2x^3$
$0=(-x+2)x^3$
$x_1=0$ und $x_2=2$
Extrema
$f'(x)=-4x^3+6x^2$
Aus $f'(x)=0$ erhalten wir die Gleichung
$0=-4x^3+6x^2$
$0=(-4x+6)x^2$
Und somit die Lösungen $x_1=0$ und $x_2=\frac 32$
Bei $x_1$ und $x_2$ ist die Tangente waagerecht, aber nur bei $x_2$ ist ein Extremum.
Bei $x_1$ ist ein Sattelpunkt (aber das war nicht gefragt).
Da Punkte gefragt waren, muss man noch die $y$-Werte bestimmen:
$N_{1,2,3}(0|0)$, $N_4(2|0)$, $E_1(0|0)$, $E_2\left(\frac 3 2|\frac{27}{16}\right)$
Die Tangente geht durch $P(1\mid f(1))=(1\mid 1)$
Die Tangenten-Steigung ist $m=f'(1)=2$.
Somit ist die Tangente: $g:\ y=2x-1$
$f'(2)=-8$
Die Normale bei $x=2$ hat somit die Steigung: $-\frac{1}{-8}=\frac18$.

Normalengleichung
$P(2\mid f(2))$ und $m=\frac18$
$f(2)=0$
In $y=mx+b$ einsetzen: $0=\frac18 2+b$
$b=-\frac14$
Nomale: $n(x)=\frac18x-\frac14$

Aufgabe 5 - Tangenten und Symmetrie

$K$ ist das Schaubild der Funktion $f$ mit $f(x)=x^3-6x^2+9x$; $x\in \mathbb R$.

Zerlegen Sie $f(x)$ in Linearfaktoren und zeichnen Sie $K$.
Bestimmen Sie die Gleichung der Tangente an $K$ in $x=2$.
Zeichnen Sie diese Tangente in das Koordinatensystem von Teilaufgabe $a)$.
Bestimmen Sie $B(u|f(u))$ so, dass die Tangente an $K$ in $B$ parallel zur Tangente an $K$ im Ursprung ist.
An welcher Stelle hat $K$ die kleinste Steigung?

Lösungen

Die Nullstellen sind $x_1=0$ und $x_{2,3}=3$
Somit gilt: $f(x)=x(x^2-6x+9)=x(x-3)^2$
$y$-Wert: $f(2)=2$
Steigung:
$f'(x)=3x^2-12x+9$
$m=f'(2)=-3$

$y$-Achsen-Abschnitt ($b$): $y=mx+b$
$2 = -3\cdot 2+b$
$b=8$
Tangentengleichung: $t:y=-3x+8$
$m=f'(0)=9$
Ansatz $f'(u)=9$

$3u^2-12u+9=9$
$3u^2-12u=0$
$3u(u-4)=0$
$u_1=0$, $u_2=4$
Die Punkte mit parallelen Tangenten mit der Steigung 9 sind:
$B_1(0|0)$ und $B_2(4|4)$
Die Frage ist also, wo $f'(x)$ minimal ist.
Die Steigung von $f'$ muss also 0 sein.
Ansatz $f''(x)=0$
$f'(x)=3x^2-12x+9$
$f''(x)=6x-12$
Mit $f''(x)=0$ erhalten wir:
$6x-12=0$
$x=2$
Da $f'(x)$ eine nach oben geöffnete Parabel ist, ist bei $x=2$ der Scheitel und somit ist $f'(2)=-3$ die minimale Steigung.
Man kann auch mit $f'''(x)$ überprüfen ob es ein Tiefpunkt von $f'$ ist.