Wendepunkte

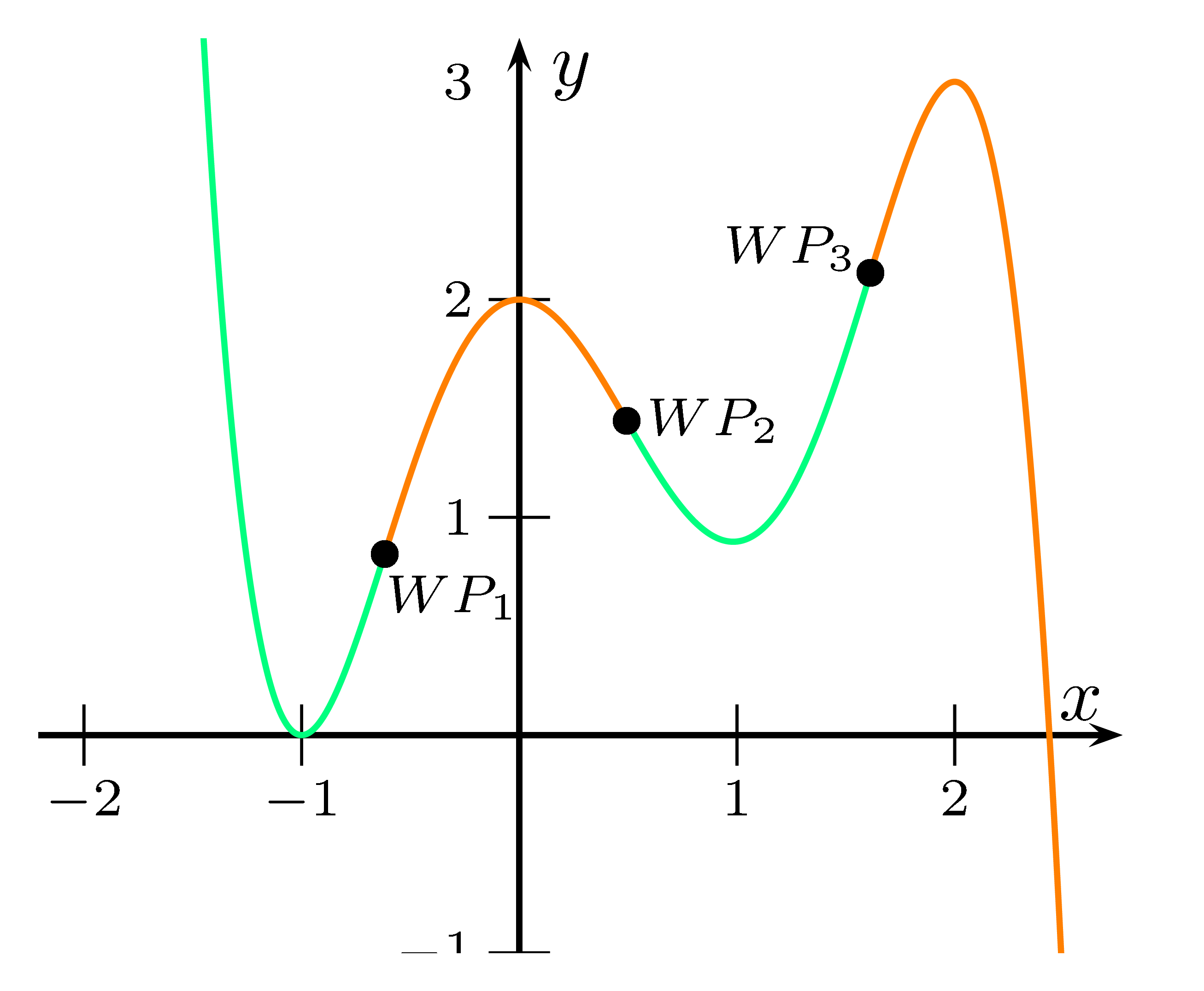
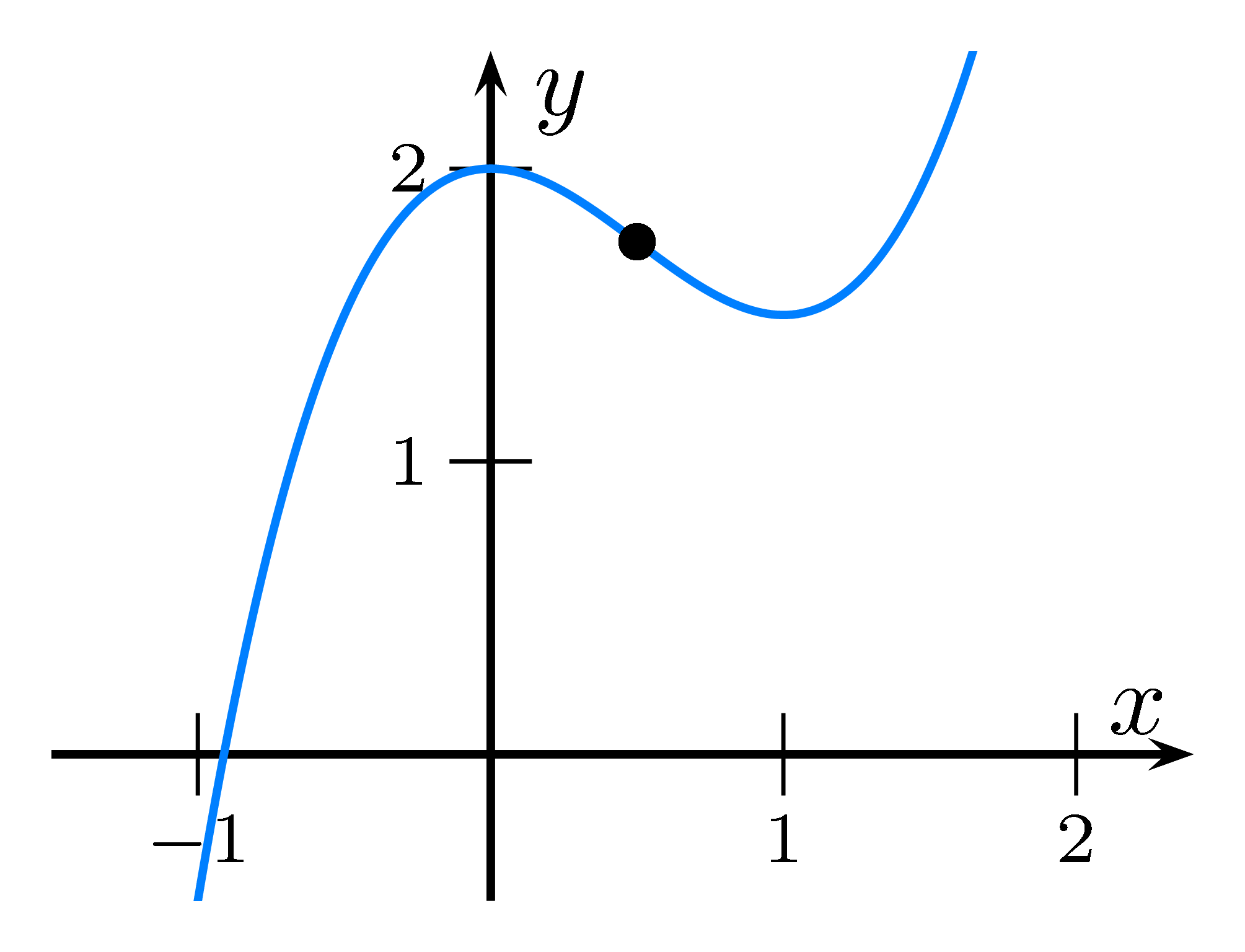
Ein Wendepunkte ist ein Punkt auf dem Graph der Funktion, wo sich die Krümmung ändert. Das Schaubild geht also von einer Rechts- in eine Linkskurve über oder von einer Links- in eine Rechtskurve.
Der Graph ist rechtsgekrümmt, wenn die zweite Ableitung negativ ist (also $f''(x)\lt 0$) und linksgekrümmt wenn $f''(x)\gt 0$.
Ein Wendepunkt liegt also vor, wenn die zweite Ableitung eine Nullstelle mit Vorzeichenwechsel hat.

Graphisch geht das Schaubild hierbei von einer Links- in eine Rechtskurve über (oder umgekehrt). Wenn man die Kurve in Gedanken mit einem Auto entlangfährt, dann ist das Lenkrad in der Rechtskurve nach rechts eingeschlagen und in einer Linkskurve nach links.
Am Wendepunkt sieht man am Lenkrad einen Übergang von einem Einschlag nach rechts zu einem Einschlag nach links.
Der Punkt an dem das Lenkrad gerade steht, ist der Wendepunkt.

Eine Funktion mit 3 Wendepunkten — Funktionsgraph mit 3 Wendepunkten.
Grün ist linksgekrümmt und rot ist rechtsgekrümmt,.

Wendepunkte berechnen

Um den Wendepunkt zu berechnen

Setzt man $f''(x)=0$
Prüft man ob $f''$ an dieser Stelle einen Vorzeichenwechsel macht (notwendiges Kriterium)
oder
prüft ob die 3. Ableitung ungleich 0 ist, also ob $f''$ steigt/fällt (hinreichendes Kriterium).
Berechnet den $y$-Wert des Wendepunkts mit $f(x)$

Gegeben: Die Funktion $f$ mit $f(x)=-\frac13x^3+1$.
Gegeben: Das Schaubild heißt $K_f$.
Gesucht: Der Wendepunkt von $K_f$.
Lösung:
1. 3 mal ableiten:
  $f (x)= -\frac13x^3+1$
  $f' (x)= -x^2$
  $f'' (x)= -2x$
  $f'''(x)= -2$
2. 2. Ableitung gleich 0 setzen
  $\begin{array}{rcll} f''(x)&=&0\\ -2x &=&0 & \ | :(-2)\\ x &=&0 \end{array}$
3. Test mit der 3. Ableitung:
  $f'''(0) = -2 \neq 0$
  Da die $f'''(0)$ nicht 0 ist liegt ein Vorzeichenwechsel vor.
  Da $f'''(0) = -2$ ist fällt $f''$ bei $x=0$ somit ist es ein Wechsel von + nach - und damit von Links- zu Rechtskrümmung.
4. $y$-Wert berechnen:
  $f(0)= 1$
  Der Wendepunkt ist somit: $WP(0\mid 1)$

Graph der Funktion mit eingezeichnetem Wendepunkt — $K_f$ mit dem $WP(0\mid 1)$

Gegeben: Die Funktion $f$ mit $f(x)=x^3-\frac32x^2+2$.
Gegeben: Das Schaubild heißt $K_f$.
Gesucht: Der Wendepunkt von $K_f$.
Lösung:
1. 3 mal ableiten:
  $f (x)= x^3-\frac32x^2+2$
  $f' (x)= 3x^2-3x$
  $f'' (x)= 6x-3$
  $f'''(x)= 6$
2. 2. Ableitung gleich 0 setzen
  $\begin{array}{rcll} f''(x)&=&0\\ 6x-3&=&0 & \ | +3\\ 6x &=&3 & \ | :6\\ x &=&\frac12 \end{array}$
3. Test mit der 3. Ableitung:
  $f'''\left(\frac12\right) = 6 \neq 0$
  Da die $f'''\left(\frac12\right)$ nicht 0 ist liegt ein Vorzeichenwechsel vor.
  Da $f'''\left(\frac12\right) = 6$ ist steigt $f''$ bei $x=\frac12$ somit ist es ein Wechsel von - nach + und damit von Rechts- zu Linkskrümmung.
4. $y$-Wert berechnen:
  $f\left(\frac12\right)= \frac74$
  Der Wendepunkt ist somit: $WP\left(\frac12\mid\frac74\right)$

Gegeben: Die Funktion $f$ mit $f(x)=x^4+x^2$.
Gegeben: Das Schaubild heißt $K_f$.
Gesucht: Wendepunkte von $K_f$.
Lösung:
1. 3 mal ableiten:
  $f (x)= x^4+x^2$
  $f' (x)= 4x^3+2x$
  $f'' (x)= 12x^2+2$
  $f'''(x)= 24x$
2. 2. Ableitung gleich 0 setzen
  $\begin{array}{rcll} f''(x)&=&0\\ 12x^2+2&=&0 & \ | -2\\ 12x^2 &=&-2 & \ | :12\\ x^2 &=&-\frac16 & \ | \pm\sqrt{\dots}\\ \end{array}$
  Unlösbar, daher hat $f''(x)$ keine Nullstellen und damit hat $K_f$ keine Wendepunkte.

Der Graph der Funktion hat keinen Wendepunkt — $K_f$

Graph der Funktion mit eingezeichneten Wendepunkten — $K_f$ mit $WP_1\left(-1\mid-\frac83\right)$ und $WP_2\left(1\mid -\frac83\right)$

Gegeben: Die Funktion $f$ mit $f(x)=\frac13x^4-2x^2-1$.
Gegeben: Das Schaubild heißt $K_f$.
Gesucht: Der Wendepunkt von $K_f$.
Lösung:
1. 3 mal ableiten:
  $f (x)= \frac13x^4-2x^2-1$
  $f' (x)= \frac43 x^3-4x$
  $f'' (x)= 4x^2-4$
  $f'''(x)= 8x$
2. 2. Ableitung gleich 0 setzen
  $\begin{array}{rcll} f''(x)&=&0\\ 4x^2-4&=&0 & \ | +4\\ 4x^2 &=&4 & \ | :4\\ x^2 &=&1 & \ | \pm\sqrt{\dots}\\ x &=& \pm1 \end{array}$
  Also ist $x_1=-1$ und $x_2=1$
3. Test mit der 3. Ableitung:
  $f'''(-1)=-8\neq 0$, somit ist bei $x_1$ ein WP
  $f'''(+1)=-8\neq 0$, somit ist bei $x_2$ ein WP
4. $y$-Wert berechnen:
  $f(-1)= -\frac83$
  $f(+1)= +\frac83$
  Die Wendepunkte sind somit: $WP_1\left(-1\mid-\frac83\right)$ und $WP_2\left(1\mid -\frac83\right)$