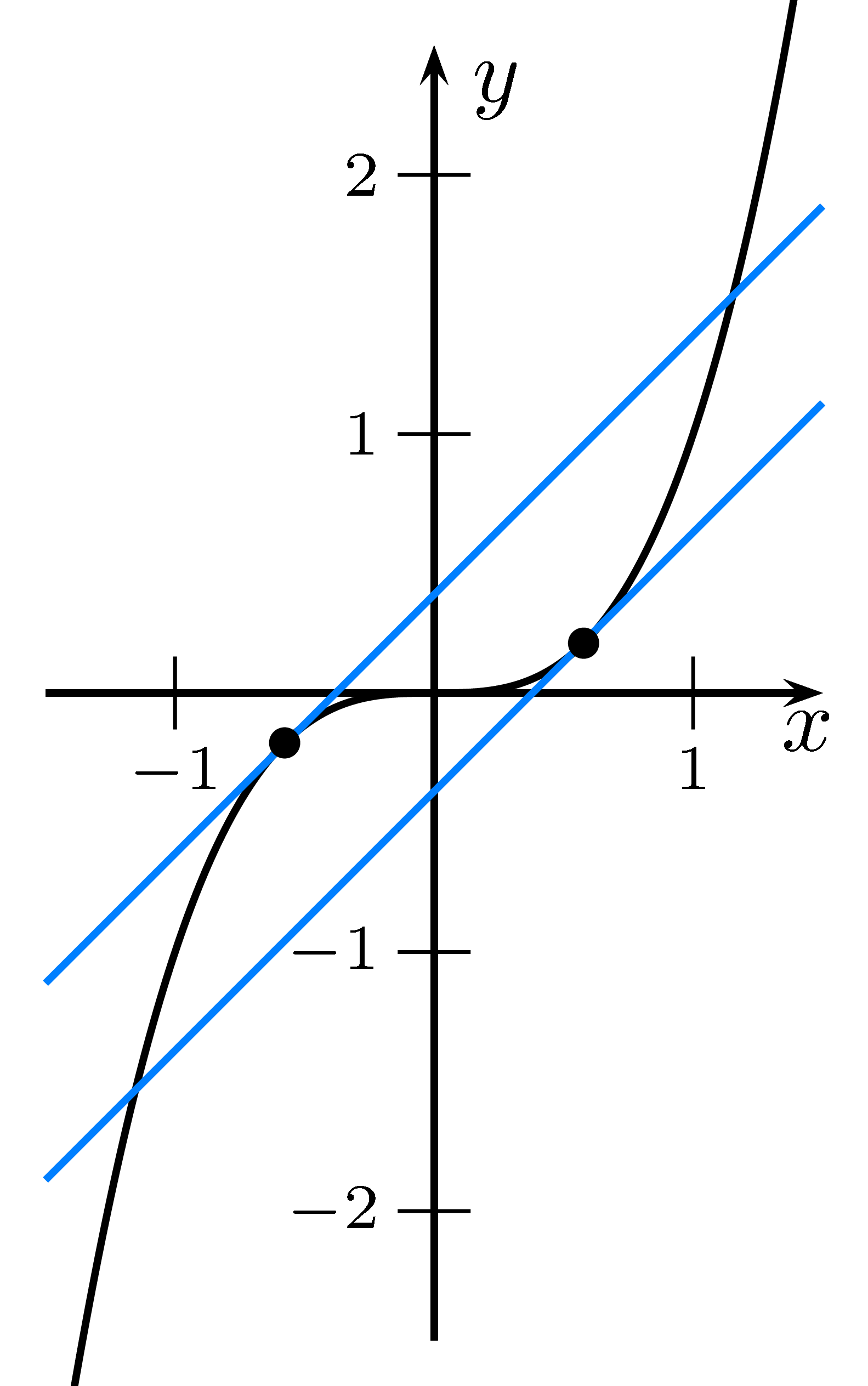
-
Gegeben: $f(x)=x^3$
Gesucht: Tangente an den Graph von $f$ mit der Steigung 1.
Lösung:- Ableitung bestimmen: $f'(x)=3x^2$
- $x$ bestimmen: $f'(x)=1$
$\begin{array}{rcl} f'(x)&=&1\\ 3x^2 &=&1\\ x^2 &=&\frac13\\ x_{1,2}&=&\pm\sqrt{\frac13}\\ x_1&\approx& -0{,}577\\ x_2&\approx& +0{,}577\\ \end{array}$ - $y$ bestimmen: $y_1=f\left(-\sqrt{\frac13} \right)=-\frac{\sqrt3}{9}$
und $y_2=f\left( \sqrt{\frac13} \right)=\frac{\sqrt3}{9}$ - In $y=mx+b$ einsetzen:
Mit $x_1$: $-\frac{\sqrt3}{9}=1\cdot \left(-\sqrt{\frac13}\right)+b$
$b=\frac{2\sqrt3}9\approx 0{,}38$
Mit $x_2$: $\frac{\sqrt3}{9}=1\cdot \left(\sqrt{\frac13}\right)+b$
$b=-\frac{2\sqrt3}9\approx -0{,}38$
- Tangenten angeben:
$t_1(x)=x+0{,}38$
$t_2(x)=x-0{,}38$