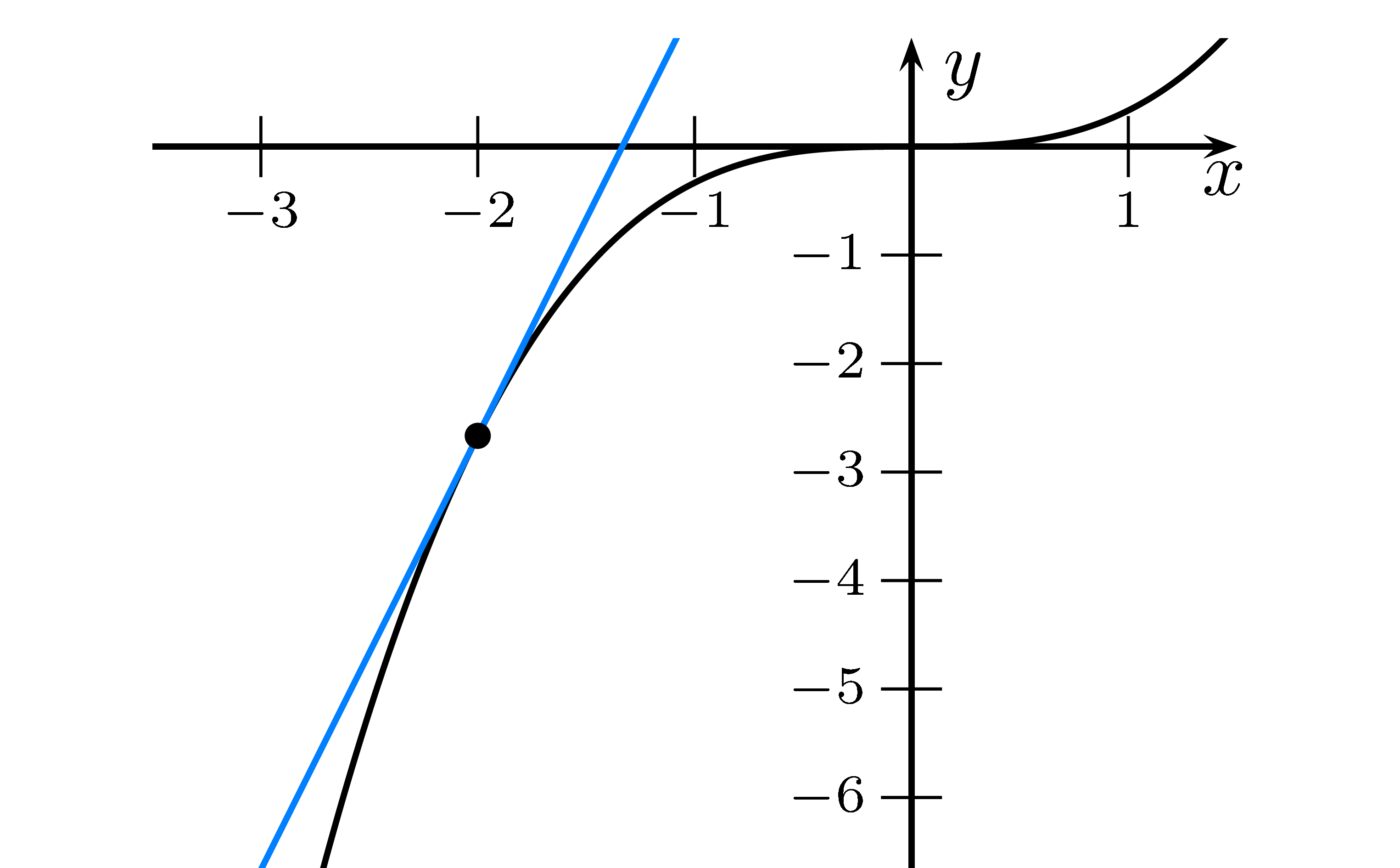
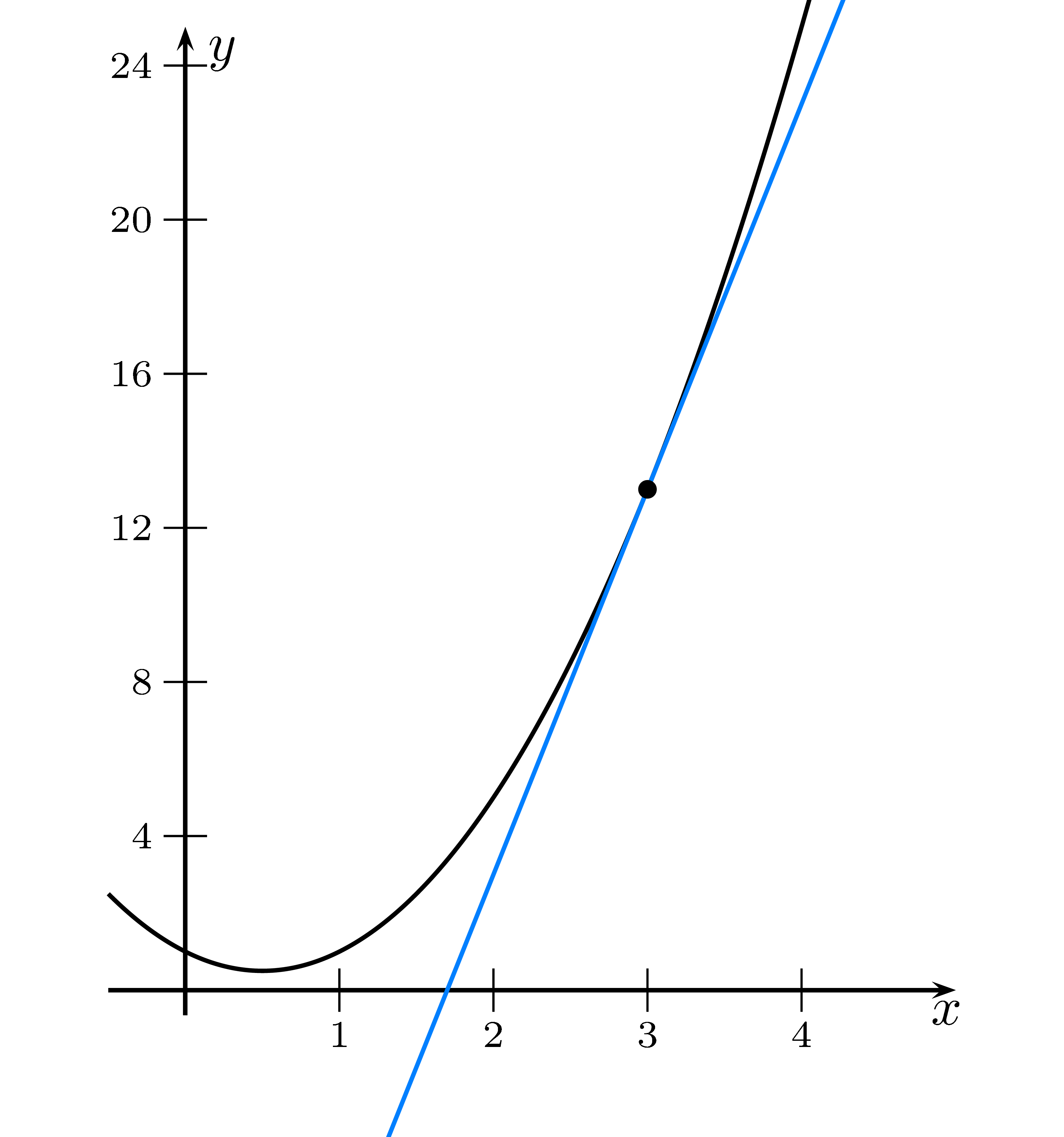
Will man die Tangente für einem bestimmten $x$-Wert $x_0$ an die Funktion $f(x)$ bestimmen,
so erhält man mit der Funktion den $y$-Wert mit $y_0=f(x_0)$ und
die Steigung der Tangente mit der Ableitung $m=f'(x_0)$.
Durch den Punkt $P(x_0\mid y_0)$ kann man mit der Steigung $m$ eine Gerade bestimmen, welche die Tangente ist.
Setzt man in $y=mx+b$ ein erhält man $y_0 = m\cdot x_0 + b$.
Hier ist nur $b$ unbekannt. Stellt man die Gleichung um erhält man $b=y_0-m\cdot x_0$.
Man kann natürlich auch die Punkt-Steigungsform für Geraden nehmen ($y=m(x-x_0)+y_0$).
Da $m=f'(x_0)$ und $y_0=f(x_0)$ ist erhält man:
Tangentengleichung: $y=f'(x_0)\cdot(x-x_0)+f(x_0)$
Ausmultipliziert erhält man: $y=f'(x_0)x-f'(x_0)x_0+f(x_0)$