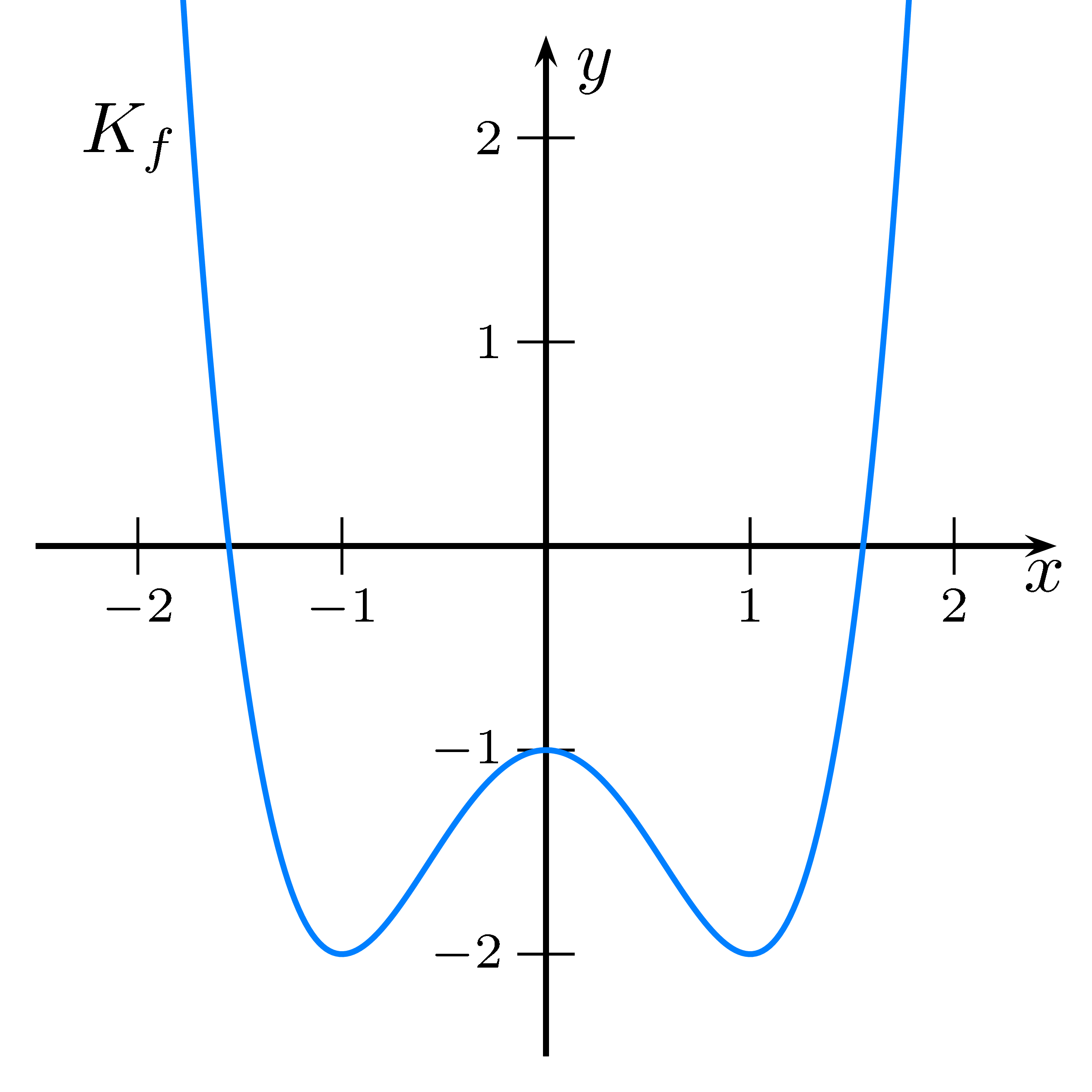
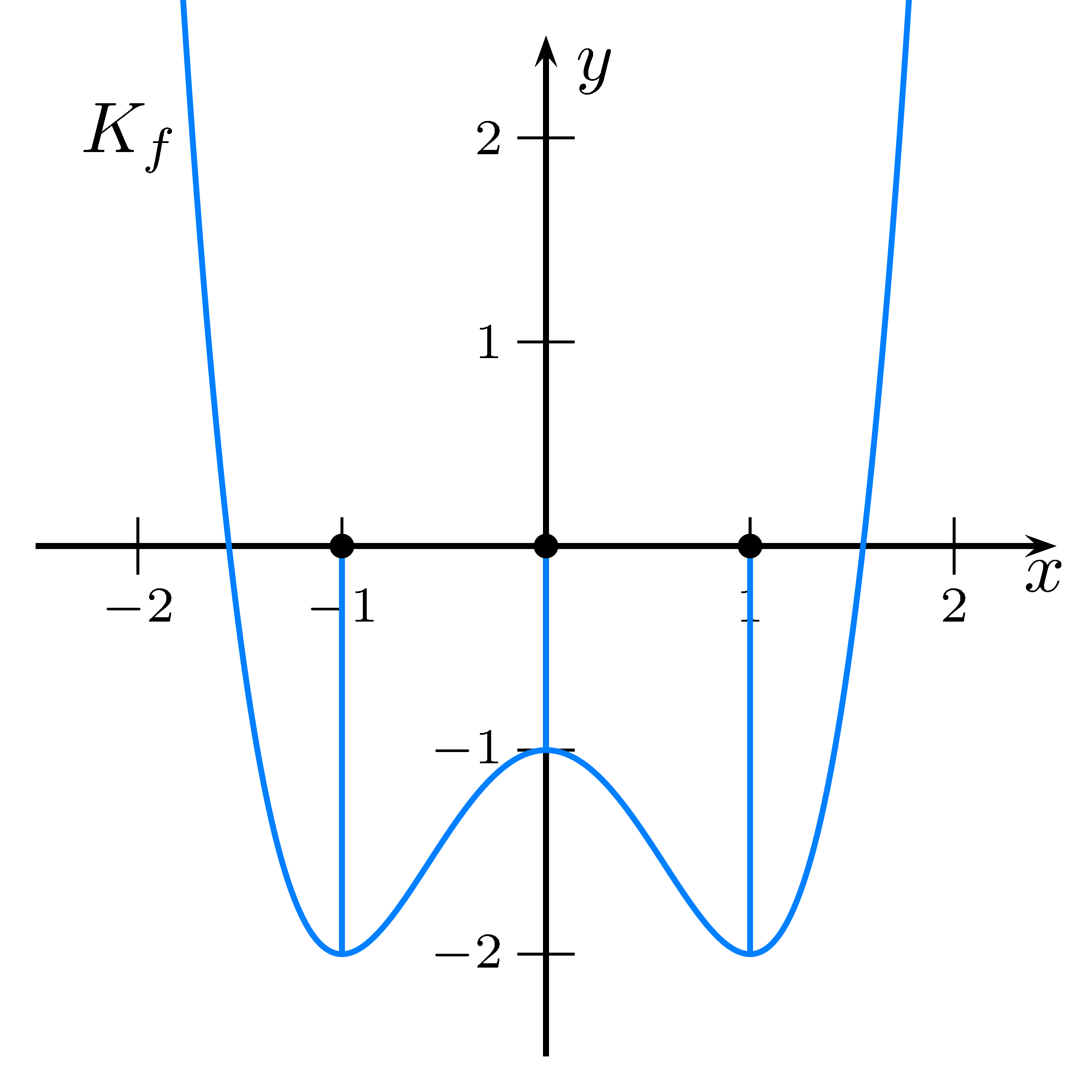
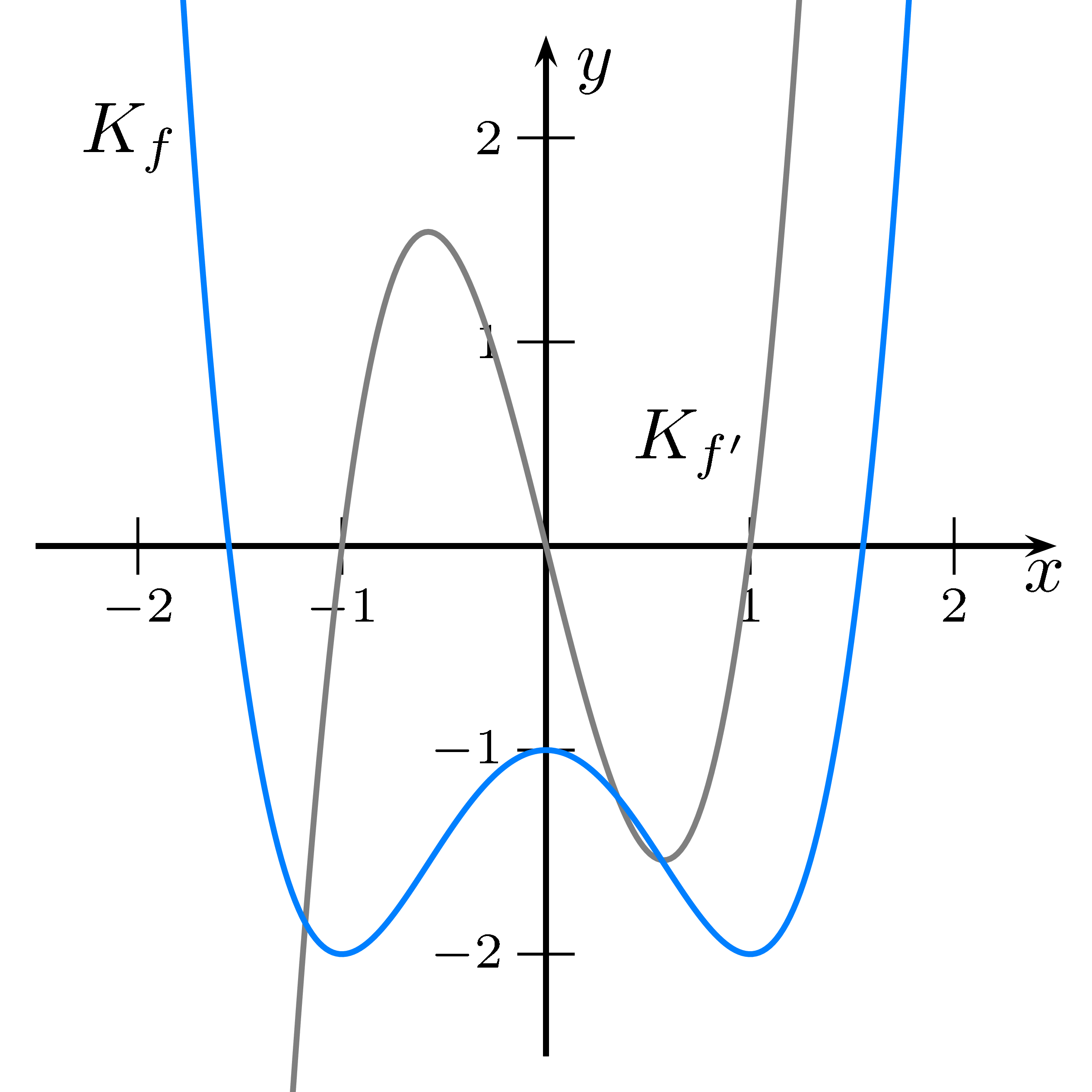
Das Schaubild der ersten Ableitung hat Nullstellen, wenn die Funktion einen Hoch- oder Tiefpunkt hat.
Der Funktionswert von $f'$ entspricht immer der Tangentensteigung am Graph von $f$.
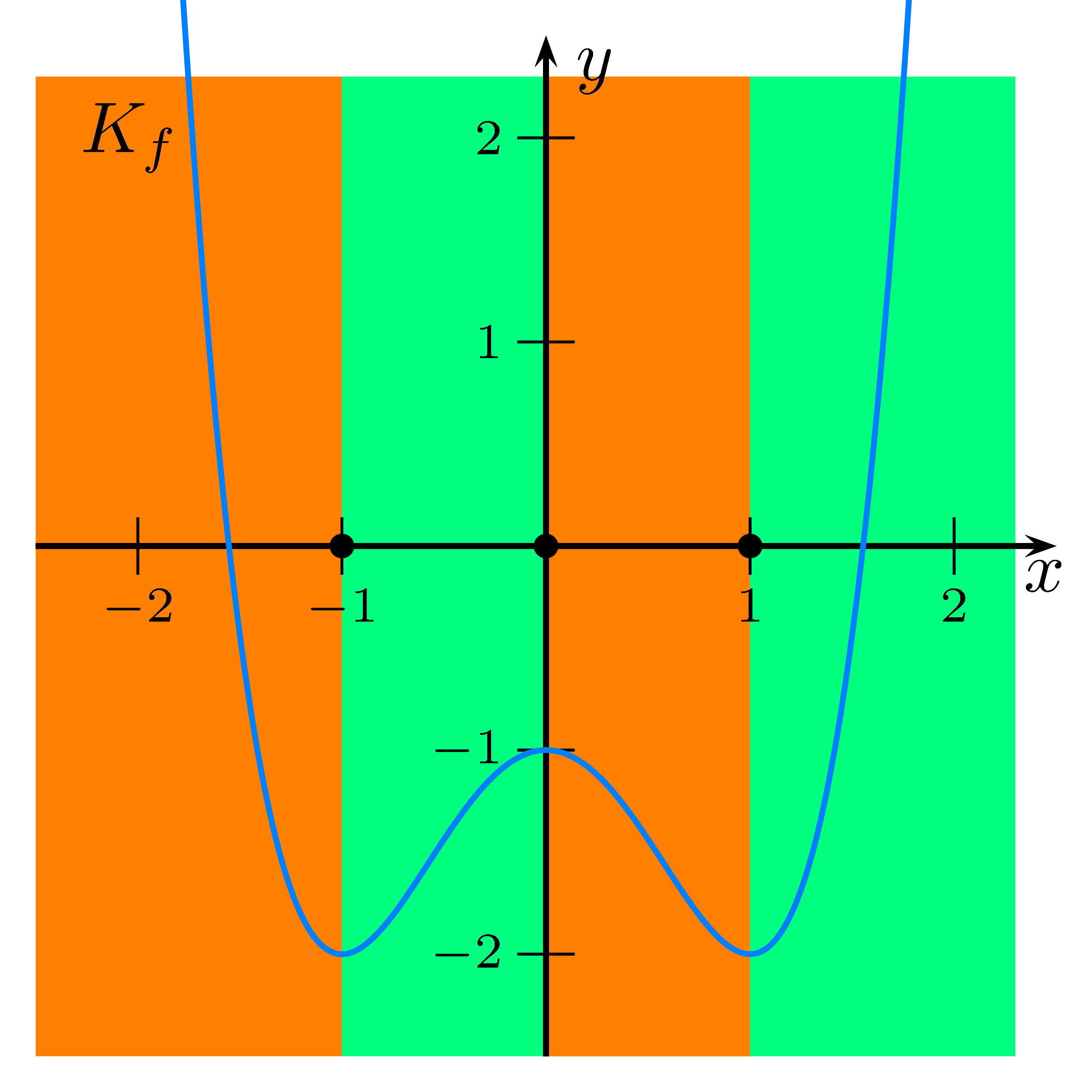
Immer wenn der Graph von $f$ fällt ist $f'$ negativ, somit ist das Schaubild von $f'$ unter der $x$-Achse.
Immer wenn der Graph von $f$ wächst ist $f'$ positiv, somit ist das Schaubild von $f'$ über der $x$-Achse.
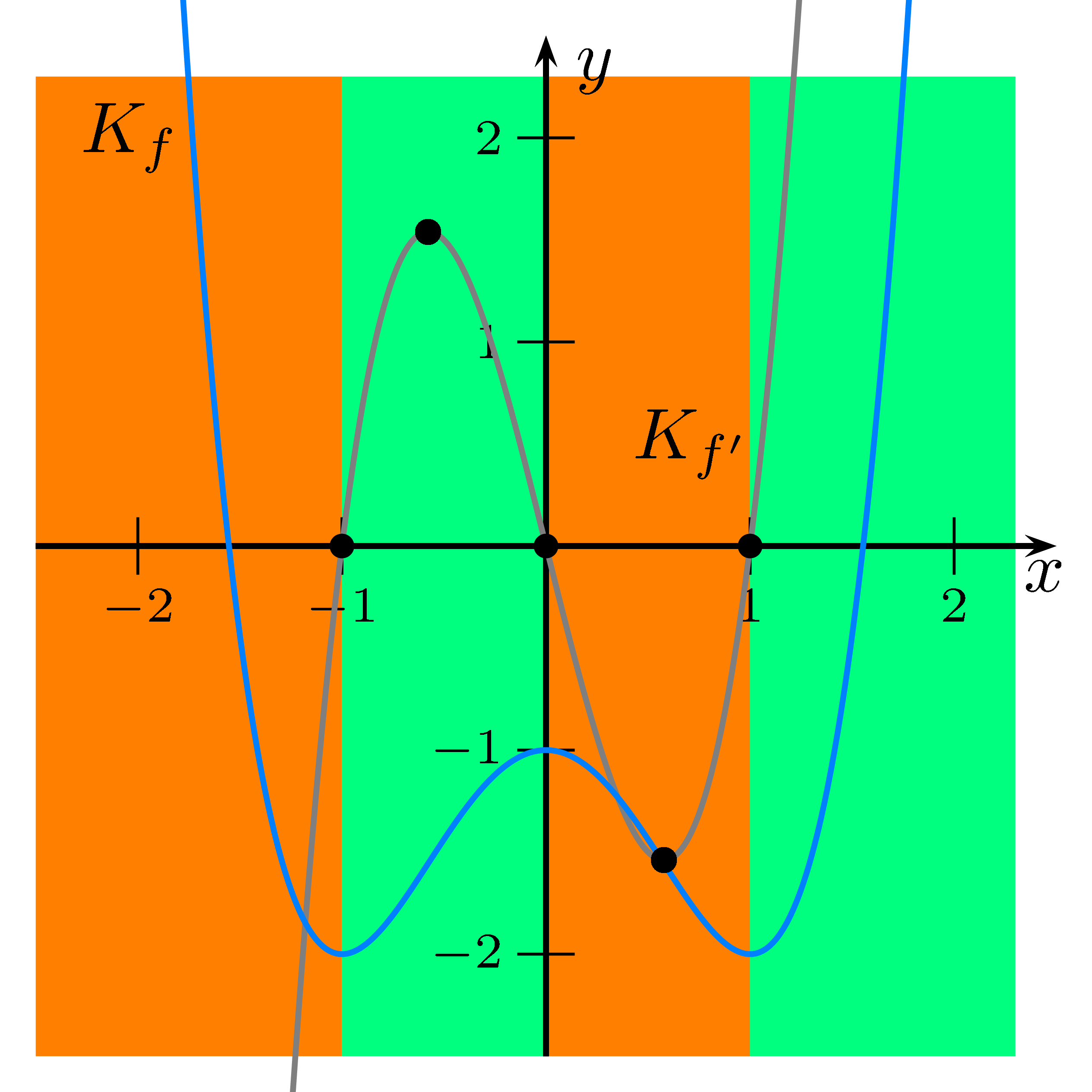
Der Funktionswert von $f'$ entspricht immer der Tangentensteigung am Graph von $f$.
Immer wenn der Graph von $f$ fällt ist $f'$ negativ, somit ist das Schaubild von $f'$ unter der $x$-Achse.
Immer wenn der Graph von $f$ wächst ist $f'$ positiv, somit ist das Schaubild von $f'$ über der $x$-Achse.
Mit diesen Kriterien kann man den Graph der ersten Ableitung gut skizzieren.