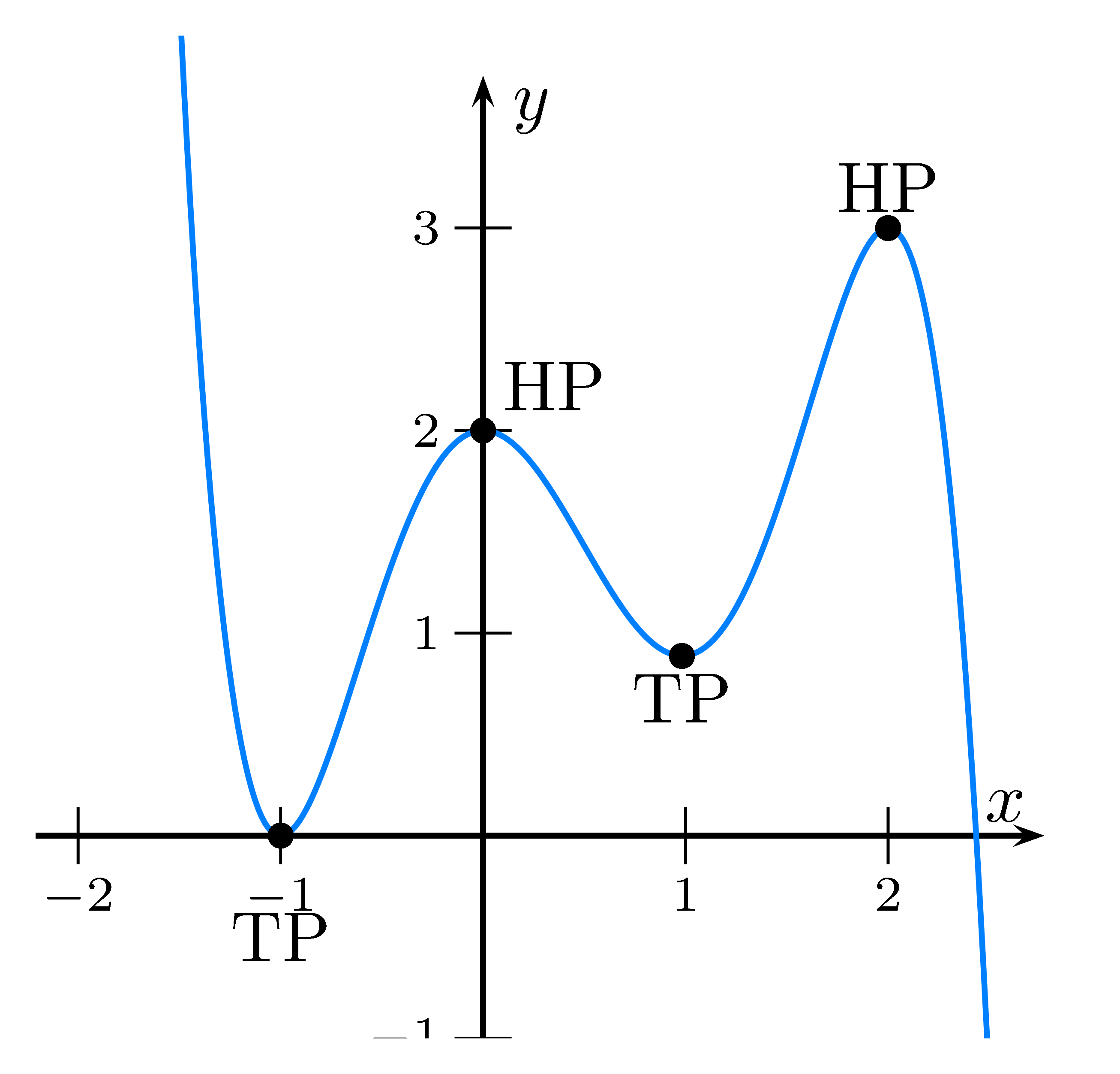
Lokale Extrempunkte oder Extrema sind die Punkte auf dem Graph einer Funktion, die
die größten oder kleinsten $y$-Werte in ihrer Umgebung haben.
Die Extrempunkte unterteilen sich in Hochpunkte und Tiefpunkte.
Die Extrempunkte unterteilen sich in Hochpunkte und Tiefpunkte.
Jeder Extrempunkt hat eine waagerechte Tangente.
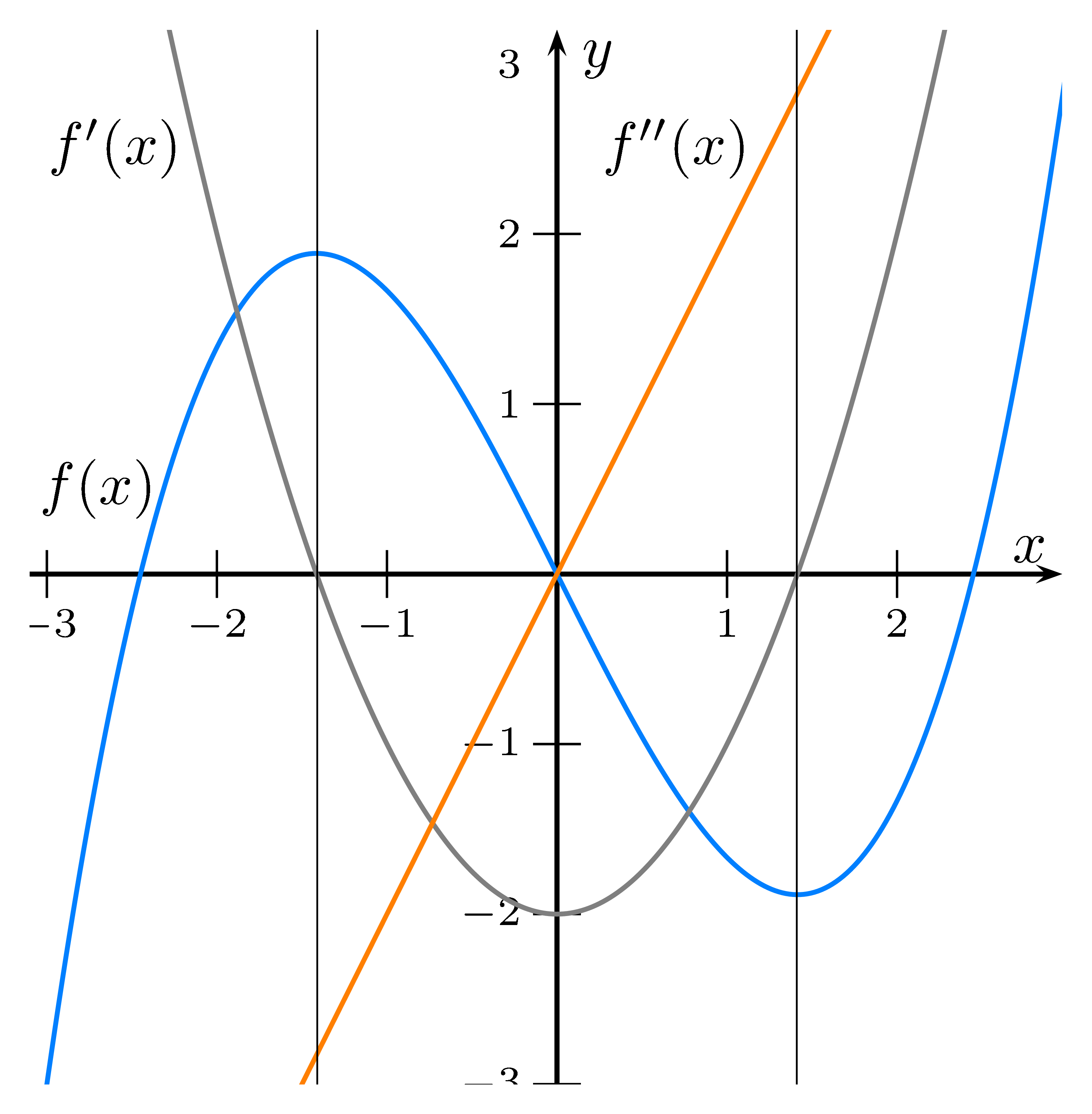
Somit gilt für jeden Extrempunkt $EP(x_1\mid y_1)$, dass $f'(x_1)=0$ ist.
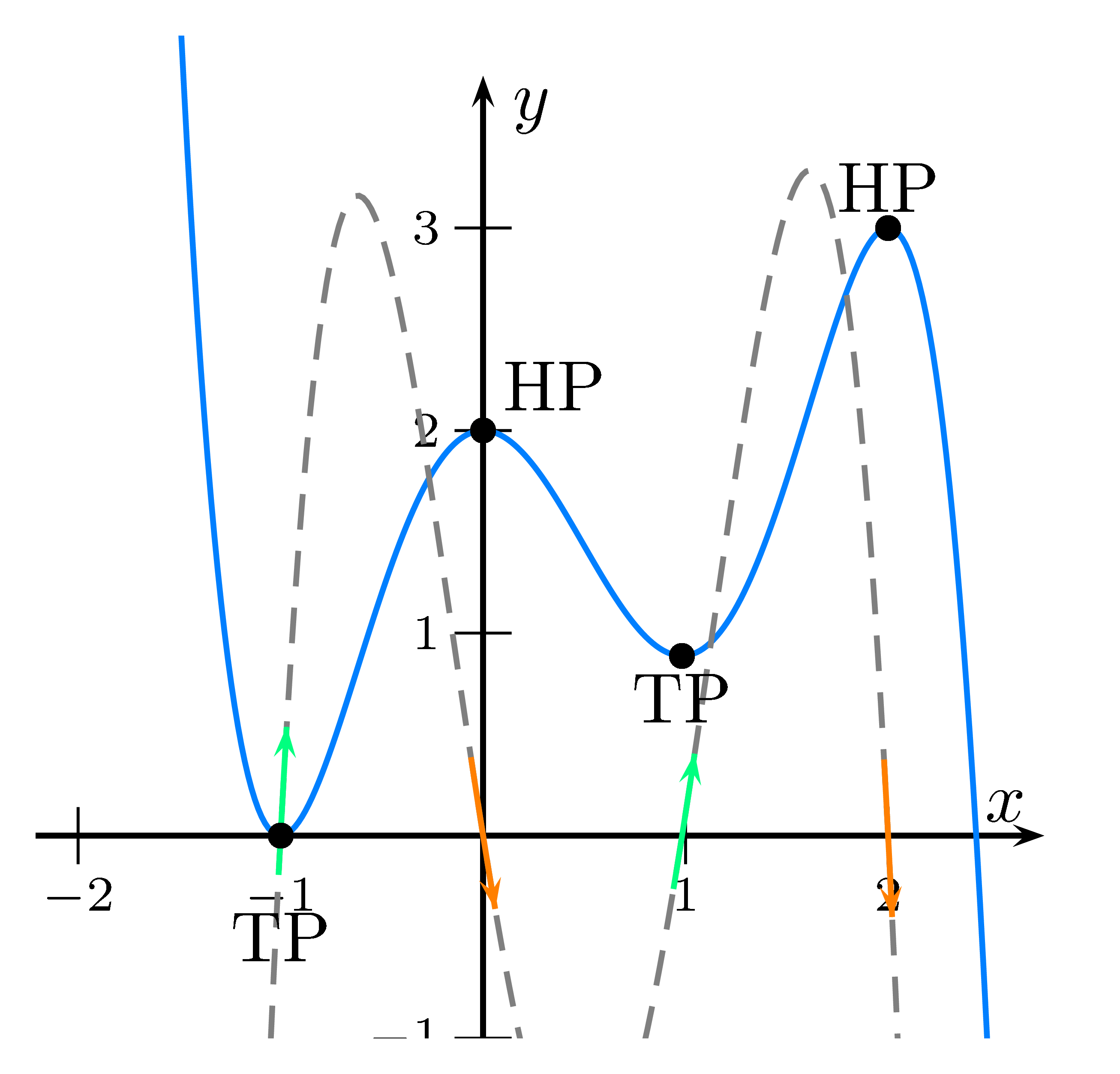
Da die Funktion vor einem Hochpunkt steigt und danach fällt hat die 1. Ableitung einen Vorzeichenwechsel von + nach -.
Dies bedeutet, dass die 1. Ableitung 0 ist und fällt.
Bei einem Tiefpunkt fällt die Funktion zuerst und steigt danach. Somit hat die 1. Ableitung einen Vorzeichenwechsel von - nach +.
Dies bedeutet, dass die 1. Ableitung 0 ist und steigt.
Da die Funktion vor einem Hochpunkt steigt und danach fällt hat die 1. Ableitung einen Vorzeichenwechsel von + nach -.
Dies bedeutet, dass die 1. Ableitung 0 ist und fällt.
Bei einem Tiefpunkt fällt die Funktion zuerst und steigt danach. Somit hat die 1. Ableitung einen Vorzeichenwechsel von - nach +.
Dies bedeutet, dass die 1. Ableitung 0 ist und steigt.