Impressum
< Index

Die zweite Ableitung

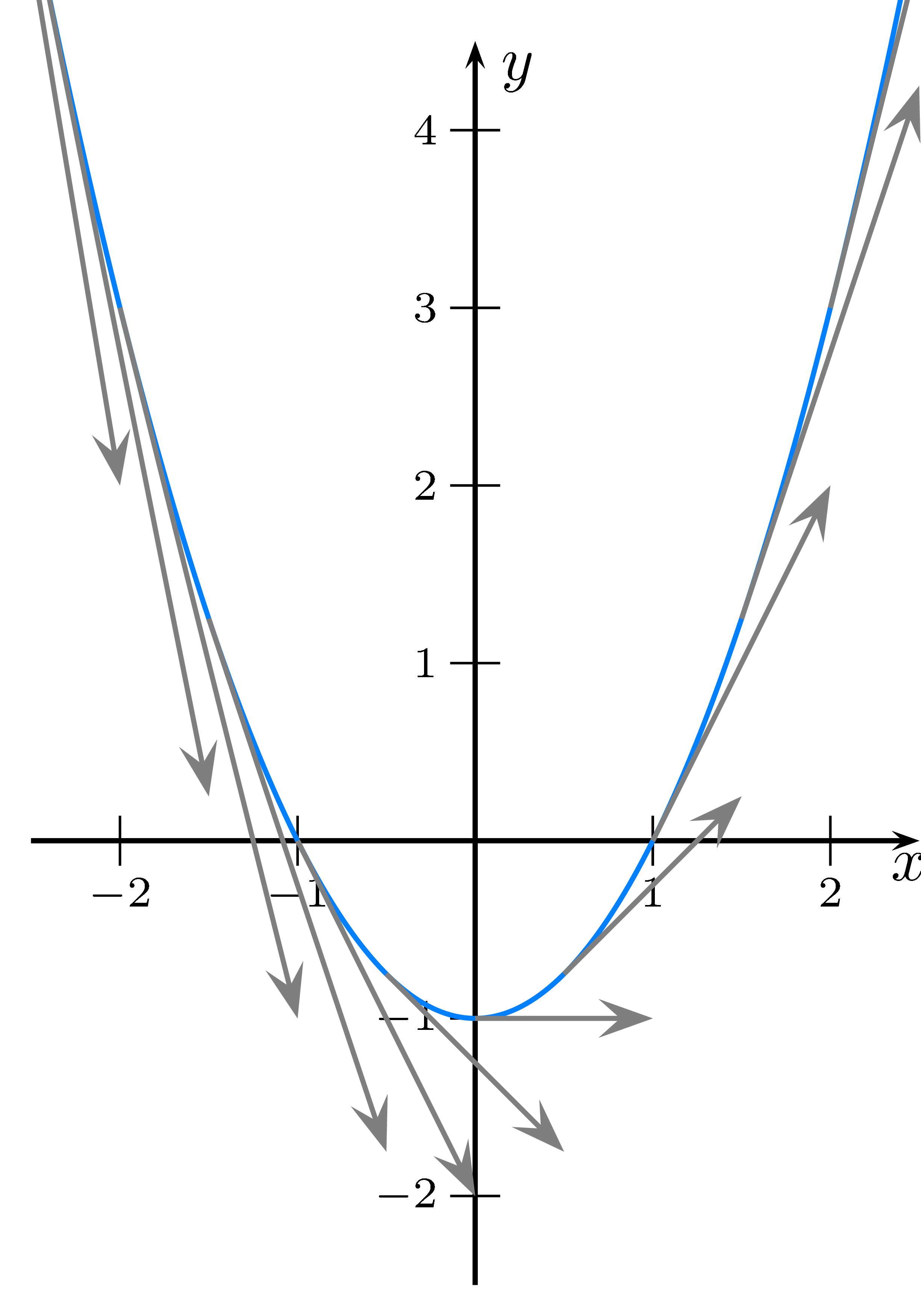
Die erste Ableitung $f'(x)$ gibt die Steigung der Funktion an.
Somit gibt die zweite Ableitung $f''(x)$ die Steigung der Steigung an.
Wenn man die Steigung als Änderung ansieht, so gibt die 2. Ableitung die Änderung der Steigung an.
Graphisch kann man sich dies wie folgt vorstellen:
  • Ist die 2. Ableitung 0, so ändert sich die Steigung nie.
    Die ist bei Geraden der Fall, hier ist $f''(x)$ immer 0.
  • Ist die 2. Ableitung größer als 0, so wird die Steigung größer.
    Die Funktion geht also immer schneller nach oben. Das Schaubild der Funktion ist dann eine Linkskurve.
  • Ist die 2. Ableitung kleiner als 0, so wird die Steigung kleiner.
    Die Funktion geht also immer schneller nach unten. Das Schaubild der Funktion ist dann eine Rechtskurve.
Parabel f(x)=x hoch 2 minus 1. Die Tangentensteigung immer mehr zu. Daher beschreibt sie eine Linkskurve.
Bei dieser Parabel mit $f(x)=x^2-1$ nimmt die Tangentensteigung immer mehr zu. Daher beschreibt sie eine Linkskurve.
Wird die Steigung größer entsteht eine Linkskurve
Wird die Steigung größer entsteht eine Linkskurve.
Wenn die Steigung zunimmt, also $f'(x)$ steigt, entsteht eine Linkskurve. Das ist genau dann der Fall, wenn $f''(x)\gt 0$ ist. Wenn die Steigung abnimmt, also $f'(x)$ fällt, entsteht eine Rechtskurve. Das ist genau dann der Fall, wenn $f''(x)\lt 0$ ist.
Wird die Steigung kleiner entsteht eine Rechtskurve
Wird die Steigung kleiner entsteht eine Rechtskurve.
Ändert die zweite Ableitung ihr Vorzeichen, so ändert der Graph der Funktion sein Kurvenverhalten.
In solchen Punkten ändert sich die Kurve also von einer Linkskurve in eine Rechtskurve oder andersherum.
Diese Punkte nennt man Wendepunkte. Man kann die $x$-Werte dieser Punkte bestimmen, indem man die Nullstellen der zweiten Ableitung bestimmt.
Wie bei der Monotonie kann man so Intervalle des Funktionsgraphen bestimmen in welchen das Krümmungsverhalten gleich bleibt. Hierzu berechnet man zuerst die Nullstellen der zweiten Ableitung und bestimmt dann für $x$-Werte zwischen diesen Nullstellen das Vorzeichen von $f''(x)$. Ist $f''(x)\gt 0$ so ist in diesem Intervall der Graph linksgekrümmt sonst rechtsgekrümmt.
Eine Kurve geht von rechtsgekrümmt in linksgekrümmt über. Das passiert bei einer Nullstelle der zweiten Ableitung mit Vorzeichenwechsel.
Bei einem Vorzeichenwechsel von $f''(x)$ ändert der Graph von $f(x)$ sein Kurvenverhalten. Hier geht er von rechts- nach linksgekrümmt.