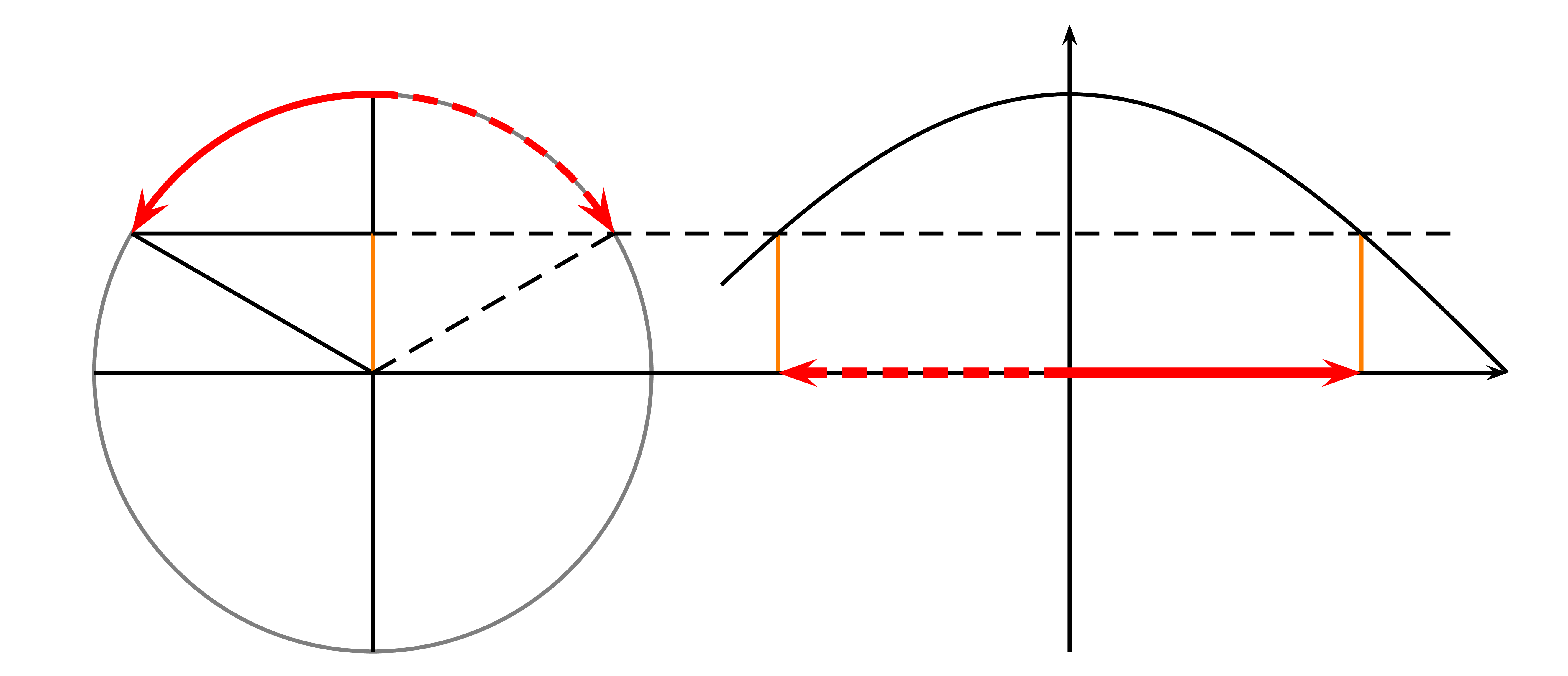
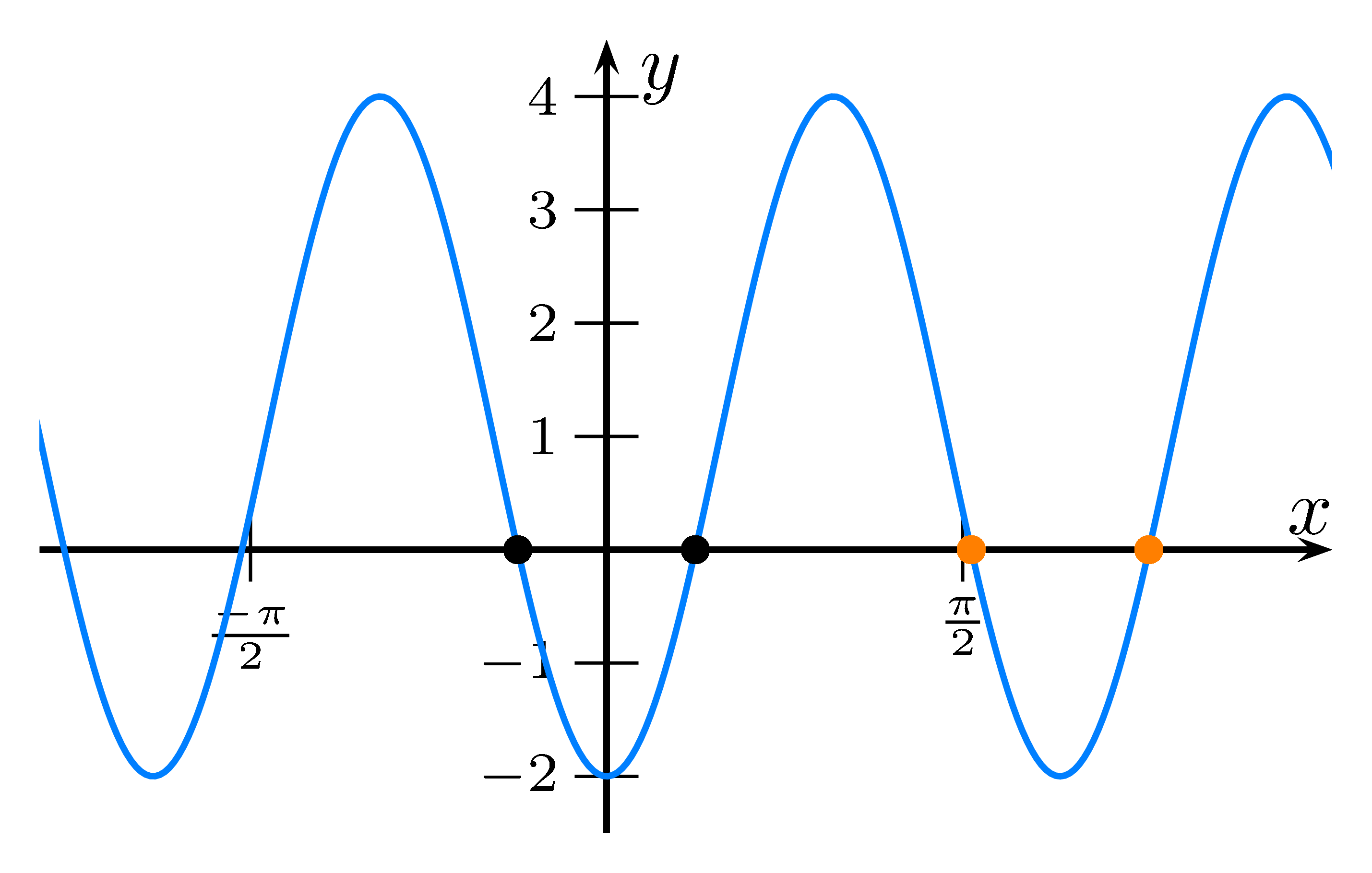
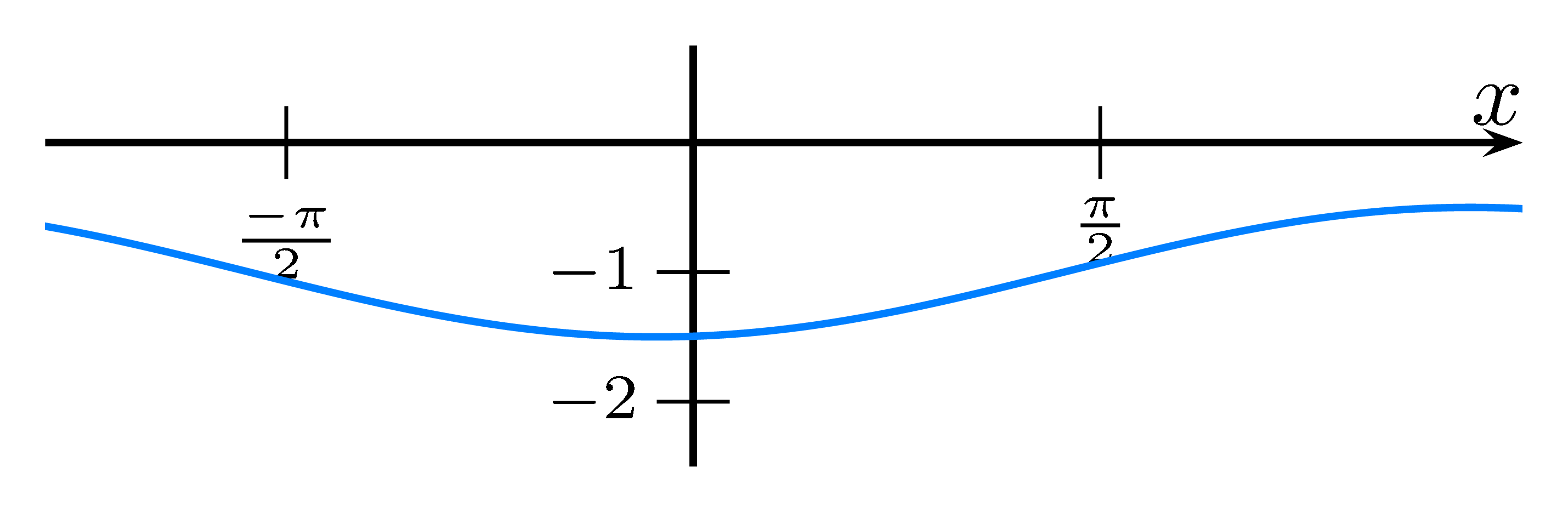
Ist der Kosinus in $y$-Richtung verschoben, so ergibt sich die Nullstelle durch Nullsetzen.
Formt man $\cos(x)+d=0$ um, erhält man $\cos(x)=-d$.
Die erste Lösung in einer Periode erhält man mittels seiner Umkehrfunktion $\cos^{-1}(-d)$, die zweite mittels $-\cos^{-1}(-d)$.
Das kann man zu $\pm\cos^{-1}(-d)$ zusammenfassen:
Die erste Lösung in einer Periode erhält man mittels seiner Umkehrfunktion $\cos^{-1}(-d)$, die zweite mittels $-\cos^{-1}(-d)$.
Das kann man zu $\pm\cos^{-1}(-d)$ zusammenfassen:
Beispiel:
$\begin{array}{rcll}
\cos(x)-\frac12 &=& 0 & \ |\ -\frac12 \\
\cos(x) &=& \frac12 & \ |\ \pm\cos^{-1}(\dots) \\
x &=& \pm\cos^{-1}(\frac12) \\
x_1 &=& \phantom{-}\frac{\pi}{3}\\
x_2 &=& -\frac{\pi}{3}
\end{array}$