Bogenmaß

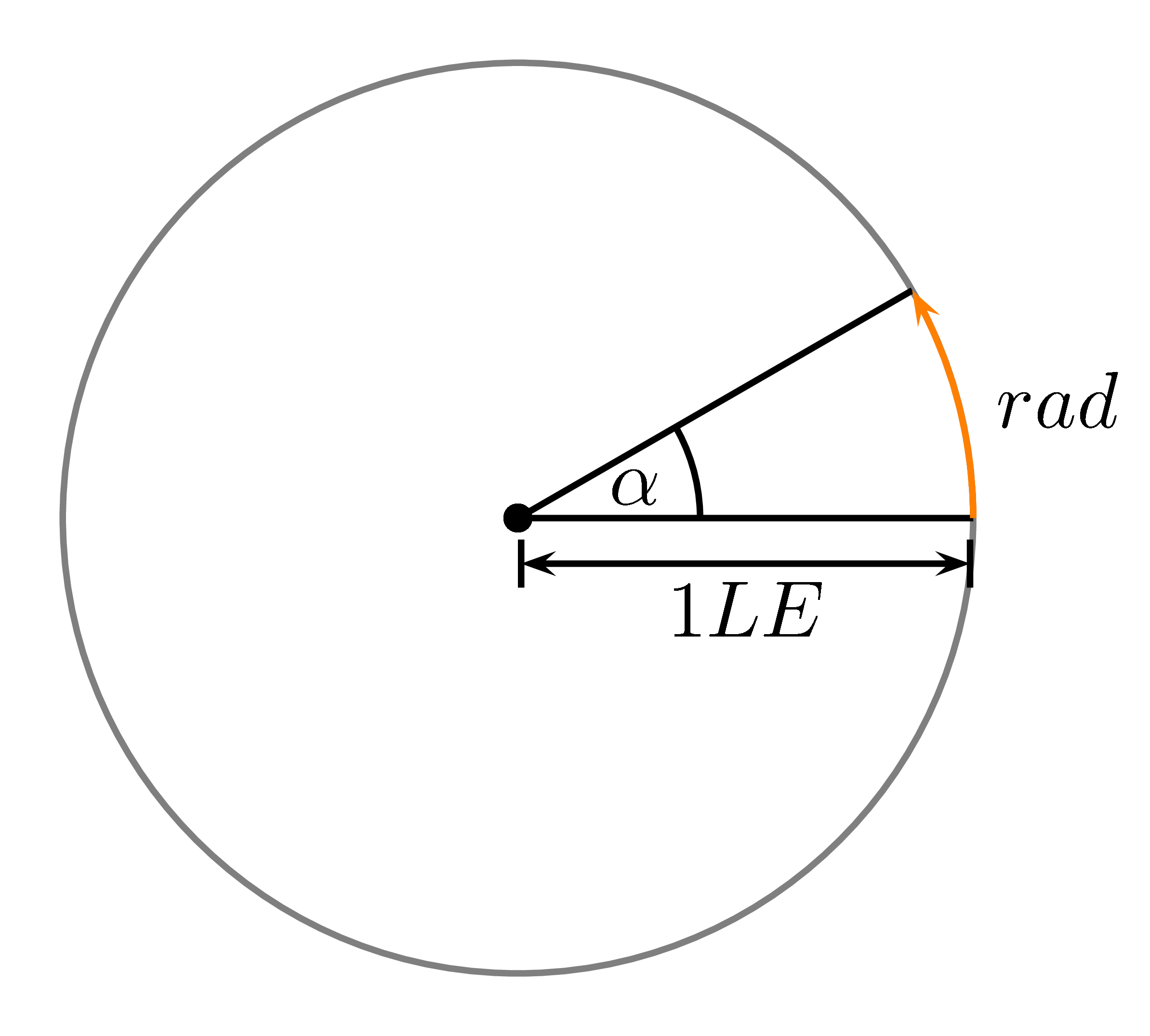
Im Bogenmaß wird der Winkel als Weglänge angegeben, die man auf dem Einheitskreis zurücklegt. Der Einheitskreis hat den Radius 1. Ein Vollwinkel hat $2\pi$, also den Umfang des Einheitskreises.

Anstatt einen Vollwinkel willkürlich in 360° zu unterteilen, verwendet die Wissenschaft das Bogenmaß.

Die „normalen“ Winkel $\alpha$ werden in Grad gemessen, im Bogenmaß in rad.

Umrechnen geht wie folgt:

$rad = \dfrac{\alpha\cdot\pi}{180}$

$\alpha = \dfrac{rad\cdot180}{\pi}$

Der Vollwinkel im Bogenmaß ist $2\pi$
Der gestreckte Winkel ist $\pi$
Der rechte Winkel ist $\frac{\pi}2$
Der 45° Winkel ist $\frac{\pi}4$

1. Geben Sie 30° im Bogenmaß an.
   Lösung: $r = \dfrac{30\cdot\pi}{180} = \frac16\pi \approx 0{,}5236$
2. Geben Sie 270° im Bogenmaß an.
   Lösung: $r = \dfrac{270\cdot\pi}{180} = \frac326\pi \approx 4{,}7124$
3. Geben Sie $\frac{\pi}{12}$ in Grad an.
   Lösung: $r = \dfrac{\frac{\pi}{12}\cdot180}{\pi} = 15^\circ$
4. Geben Sie $0{,}1$ in Grad an.
   Lösung: $r = \dfrac{0{,}1\cdot180}{\pi} \approx 5{,}7296^\circ$