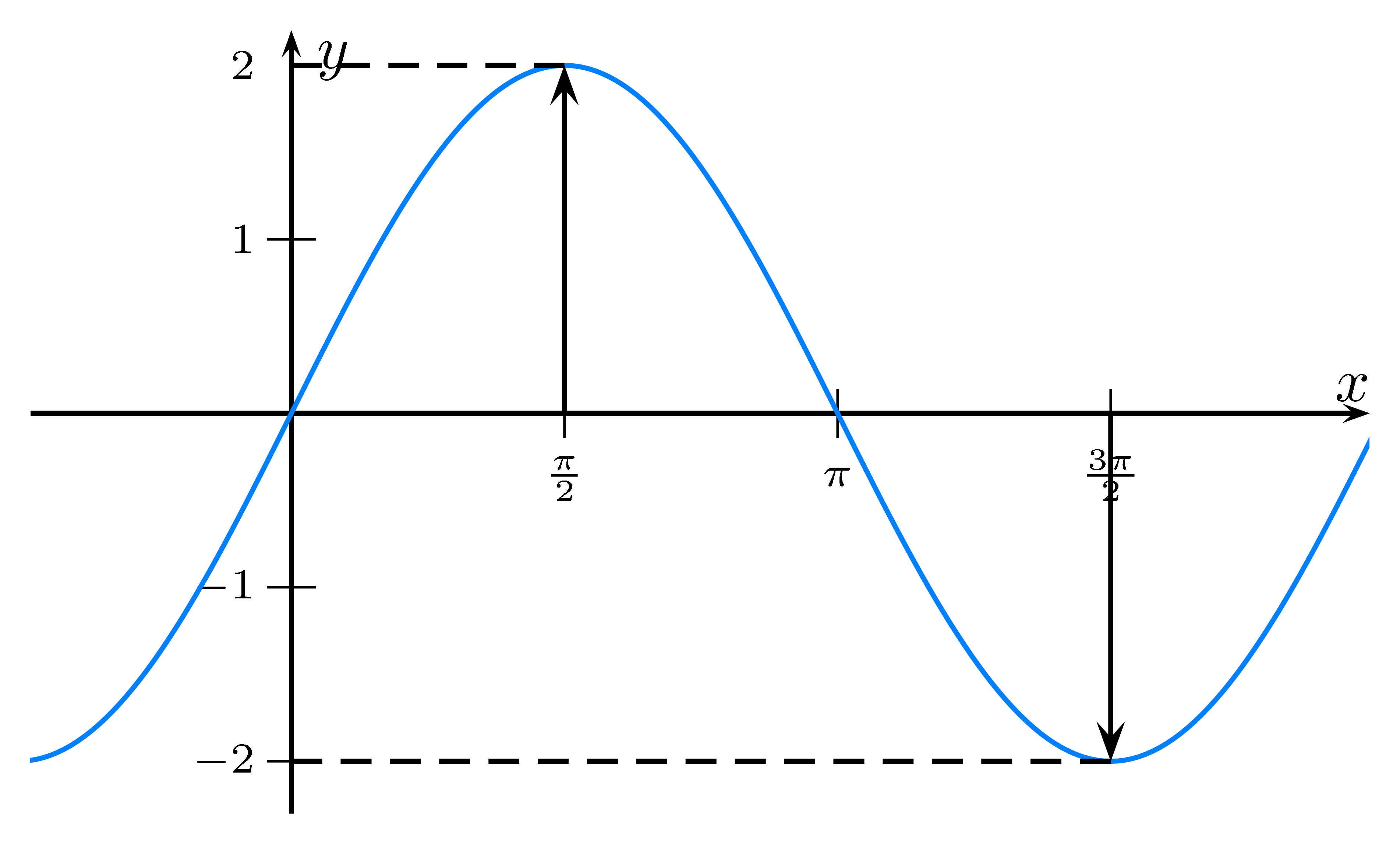
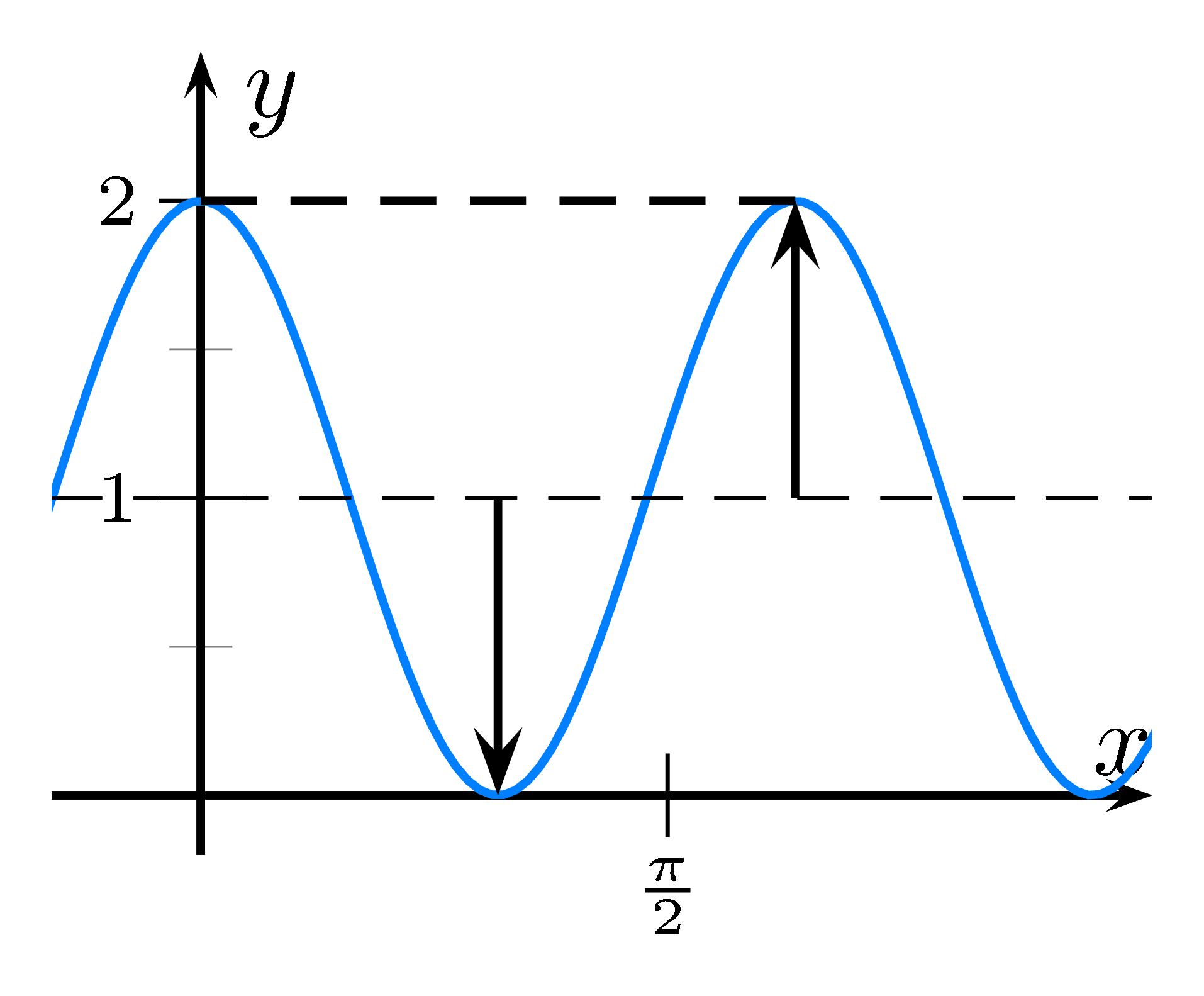
Der Graph von $f(x)=2\sin(x)$ hat einen Wertebereich von -2 bis 2.
Somit ist die Amplitude $a=\frac{2-(-2)}2 = \frac42 = 2$.
Wenn der Funktionsterm gegebenem ist, kann man es an ihm leichter ablesen. Wenn aber nur der Graph gegeben ist, muss man es so berechnen.
Somit ist die Amplitude $a=\frac{2-(-2)}2 = \frac42 = 2$.
Wenn der Funktionsterm gegebenem ist, kann man es an ihm leichter ablesen. Wenn aber nur der Graph gegeben ist, muss man es so berechnen.