Die
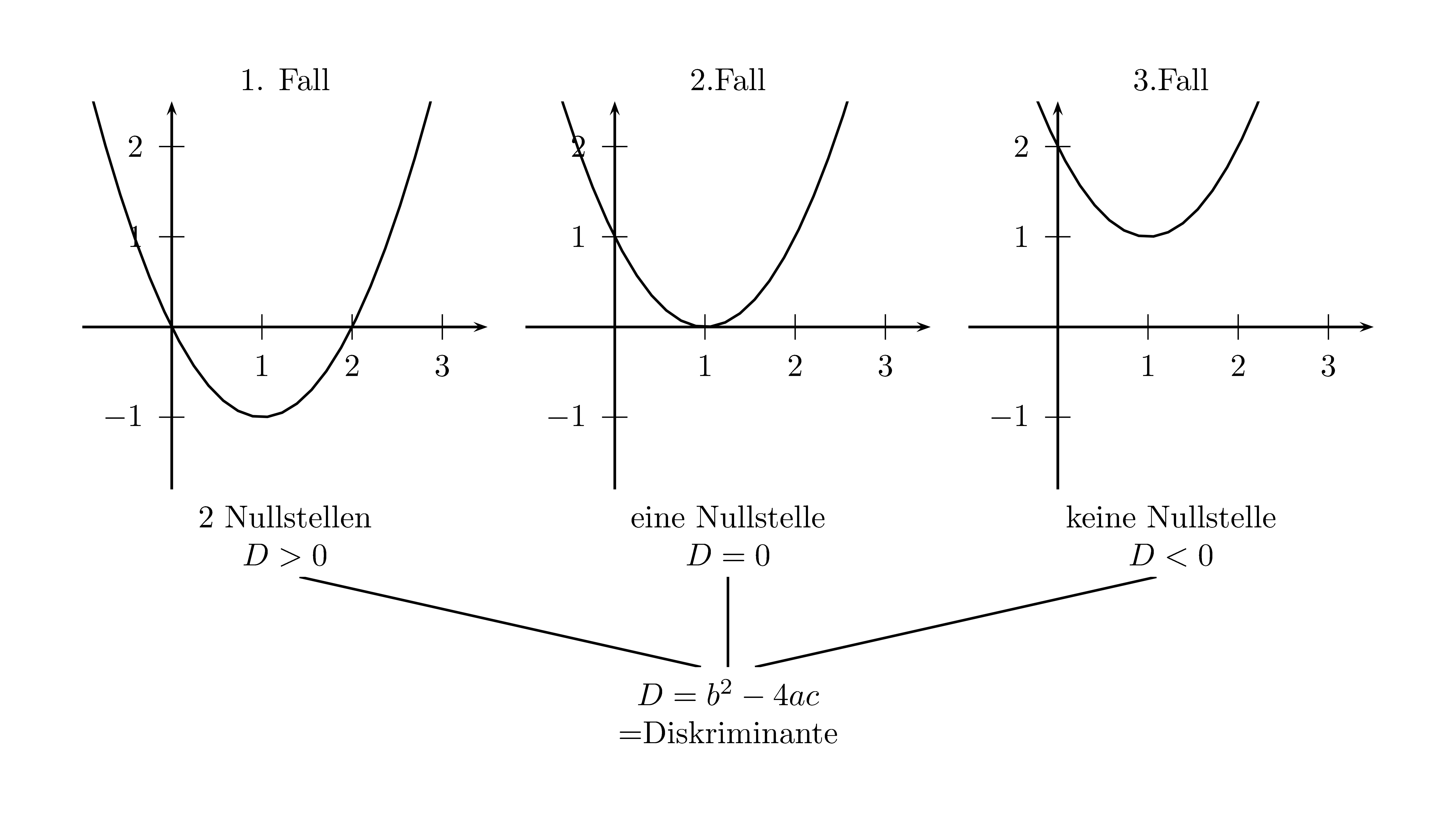
Diskriminante $D=b^2-4ac$ gibt an, wie viele Schnittpunkte eine Parabel mit der $x$-Achse hat:
- $D\lt 0$: keine Nullstelle
- $D = 0$: eine Nullstelle
- $D\gt 0$: zwei Nullstelle
Die Diskriminante ist genau der Term, der in der Mitternachtsformel unter der Wurzel steht: $x_{1,2}=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$.
Steht in der Mitternachtsformel etwas negatives unter der Wurzel, hat sie keine Lösung (keine Nullstelle), steht 0 unter der
Wurzel hat sie genau eine Lösung (eine Nullstelle bei $x=\frac{-b}{2a}$) und ist der Wert unter der Wurzel positiv, so hat
sie zwei Lösungen (zwei Nullstellen).
Hat man die Diskriminante berechnet und sie ist kleiner 0 ist man fertig.
Wenn sie positiv oder 0 ist, kann man den Wert in der Mitternachtsformel unter der Wurzel einsetzen, somit ist die
Berechnung der Diskriminante nie verschwendete Arbeit.