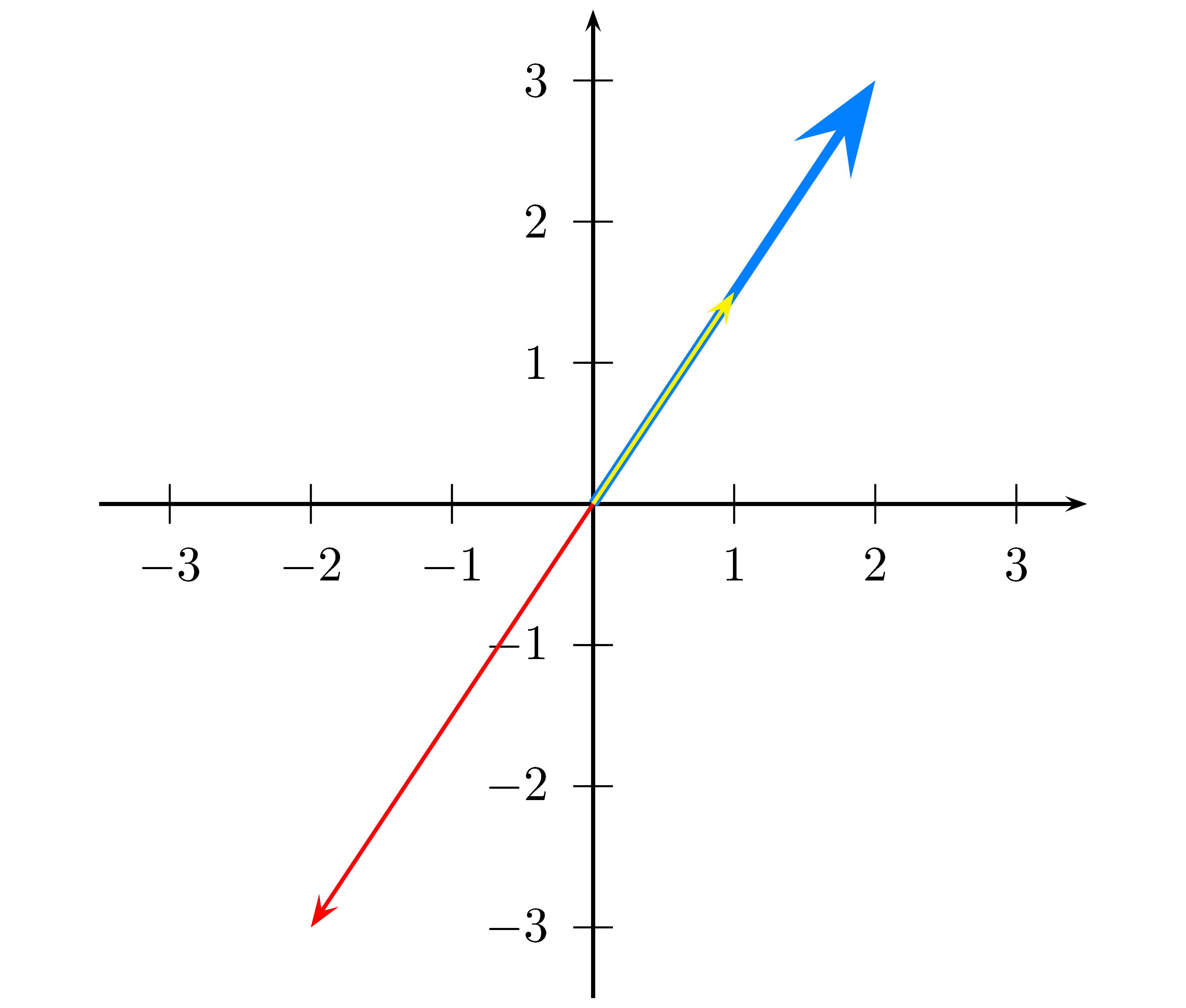
Multipliziert man einen Vektor $\vec v = \vz{x}{y}$ mit einer reelen Zahl $r$ (einem sogenannten Skalar),
so wird jede Komponente des Vektors mit $r$ Multipliziert.
$r\cdot\vz xy = \vz{r\cdot x}{r\cdot y}$
Geometrisch wird der Vektor durch die Multiplikation mit $r$
Ein Vektor und sein Gegenvektor haben die gleiche Richtung.
- gestreckt, wenn $|r|\gt1$
- gestaucht, wenn $|r|\lt1$
- ist $r\lt 0$ so kehrt sich die Richtung des Vektors um
Ein Vektor und sein Gegenvektor haben die gleiche Richtung.
Wenn zwei Vektoren die gleiche Richtung haben, sagt man dass sie linear abhängig sind.
Mathematisch ausgedrückt: Gibt es ein $r\in\mathbb{R}$, so dass $r\cdot \vec v = \vec w$, dann sind $\vec v$ und $\vec w$ linear abhängig.
Mathematisch ausgedrückt: Gibt es ein $r\in\mathbb{R}$, so dass $r\cdot \vec v = \vec w$, dann sind $\vec v$ und $\vec w$ linear abhängig.