Übungen zum Logarithmus

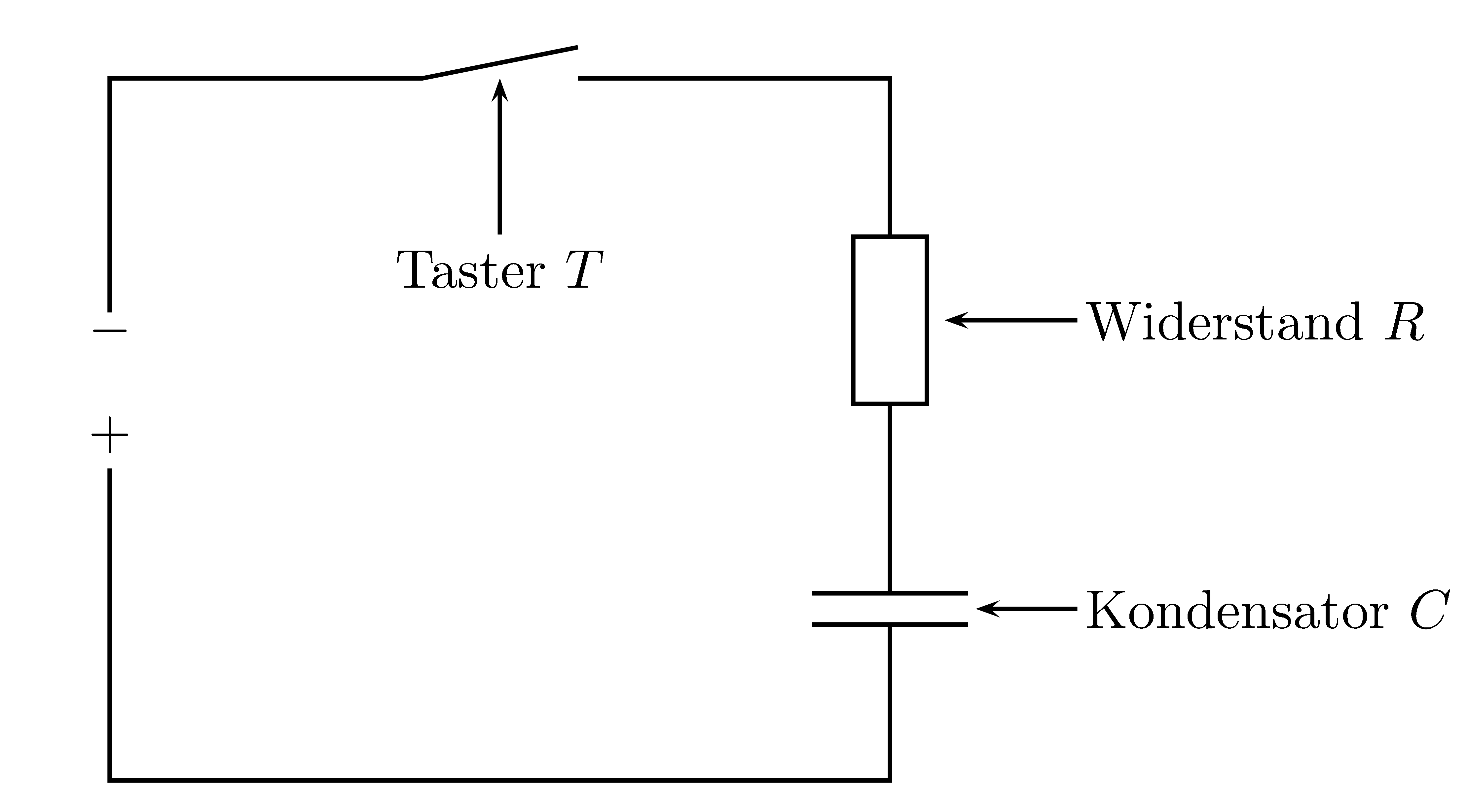
Ein begnadeter Techniker baut eine Schaltung mit einem Widerstand und einem Kondensator auf.

Der Kondensator hat $100 \mu F$,
der Widerstand hat $50\Omega$ .
Die Schaltung wird mit $9V$ betrieben.

Wenn man den Taster $T$ drückt, dann lädt sich der Kondensator $C$ auf bis er die Betriebsspannung von $9V$ erreicht.

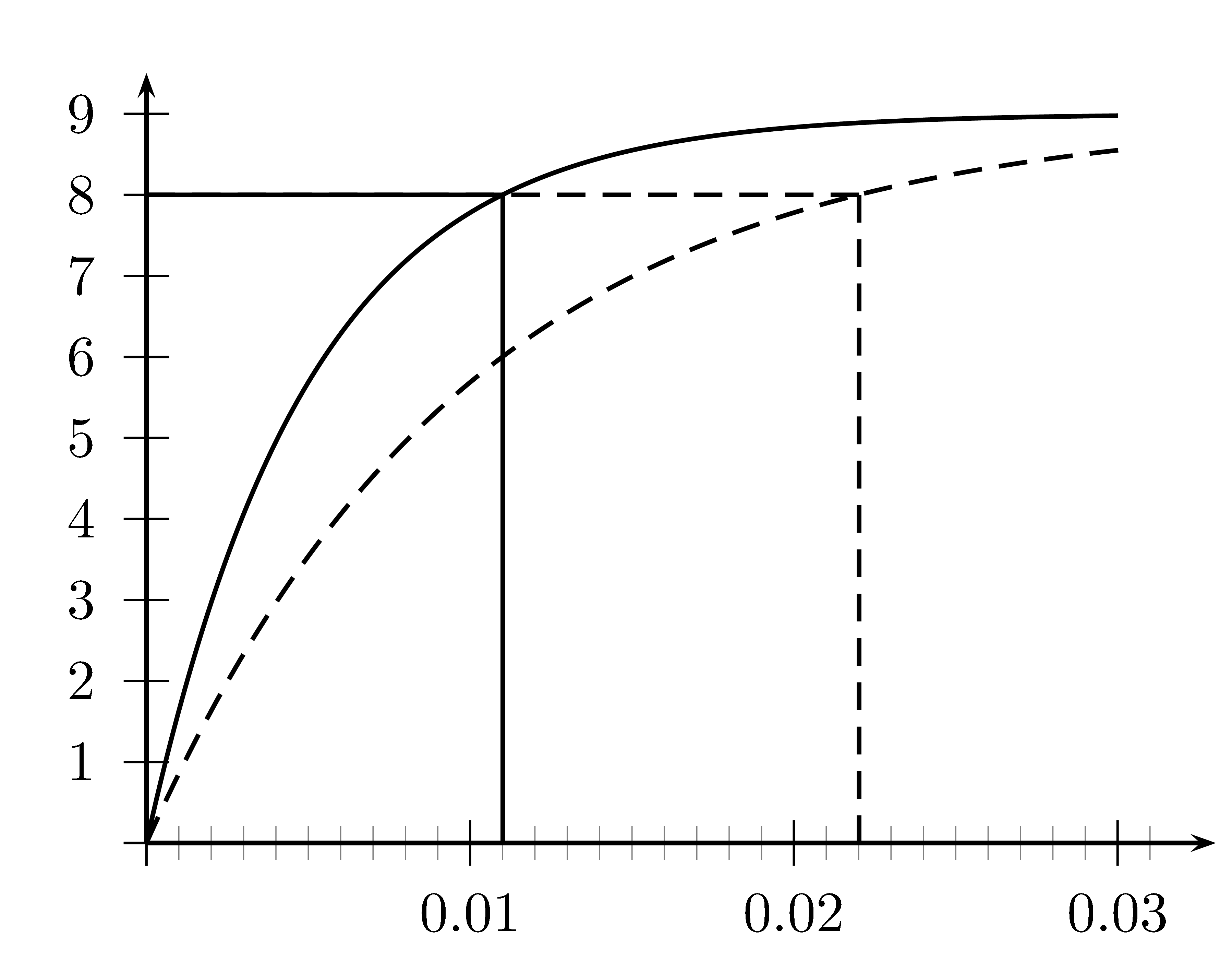
Die Spannung $U$ eines Kondensators wird wie folgt berechnet: \[ U(t)=U_s\left(1-e^{-\frac{t}{R\cdot C}}\right) \]

Aufgaben

1. Bei der gegebenen Schaltung ist $U_s=9V$, $C=100\cdot 10^{-6}F$ und $R=50\Omega$.
   Wie lange muss $T$ gedrückt werden, so dass der Kondensator eine Spannung ($U(t)$) von $8V$ aufweist.
   Hinweise

   Man hat die Funktionsgleichung $U(t)=U_s\left(1-e^{-\frac{t}{R\cdot C}}\right)$ von oben.
   Jetzt setzt man für die nervigen Buchstaben die konkreten Werte ein (in Mathe darf man die Einheiten weglassen).
   Also $U_s=9$, $C=100\cdot 10^{-6}$ (was 0,0001 ist) und $R=50$ in $U(t)$ einsetzen.
   Gesucht wird eine Dauer, also ein Wert für $t$. $U(t)$ soll ja $8V$ sein.
   Es sind nur Hinweise, den Rest sollst du jetzt selbst machen.
   
   
2. Wie lange benötigt der Kondensator um auf $8V$ zu kommen, wenn der Vorwiderstand $R=100\Omega$ hat?
3. Zeichne die Ladekurven von a) und b) in ein Schaubild ein.
   Die $x$-Achse soll von $0s$ bis $0,03s$ (in $0,01s$ entsprechen $2cm$) und
   die $y$-Achse von $0V$ bis $9V$ ($1V$ entsprechen $0,5cm$) gehen.
   Für Faule

   

   
   
4. In der Theorie (Mathe) dauert es unendlich lange bis der Kondensator vollständig geladen ist.
   In der Praxis (Technik) nimmt man als Ladezeit $t_l =5\cdot R\cdot C$.
   Wie lange ist diese Ladezeit bei den Werten aus a) und b)?
   Wie hoch ist die Spannung am Kondensator nach dieser Zeit bei a) und bei b)?