Aufgabe 1 - Punkte
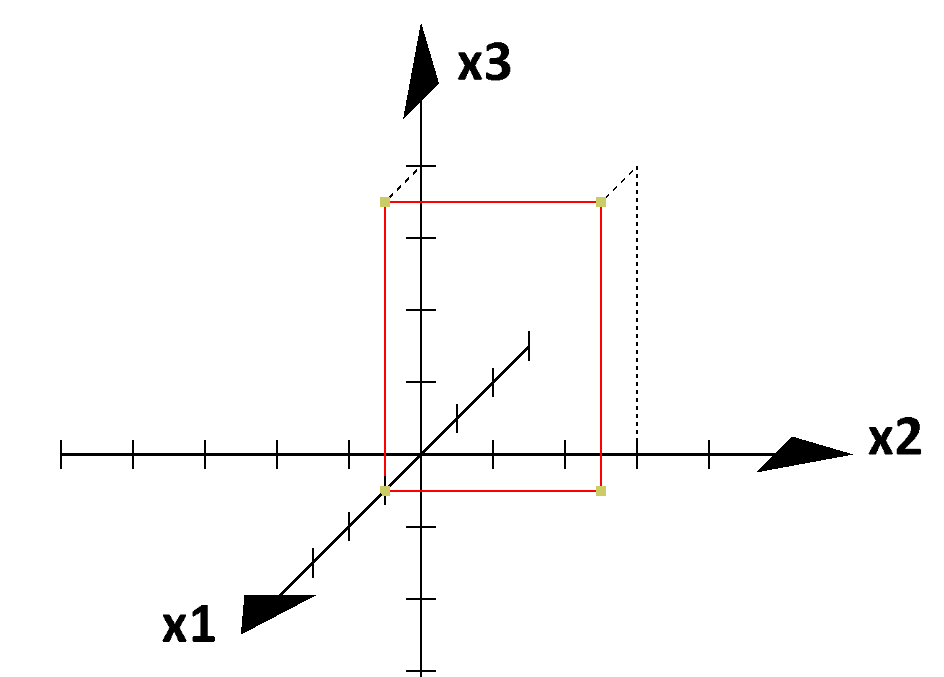
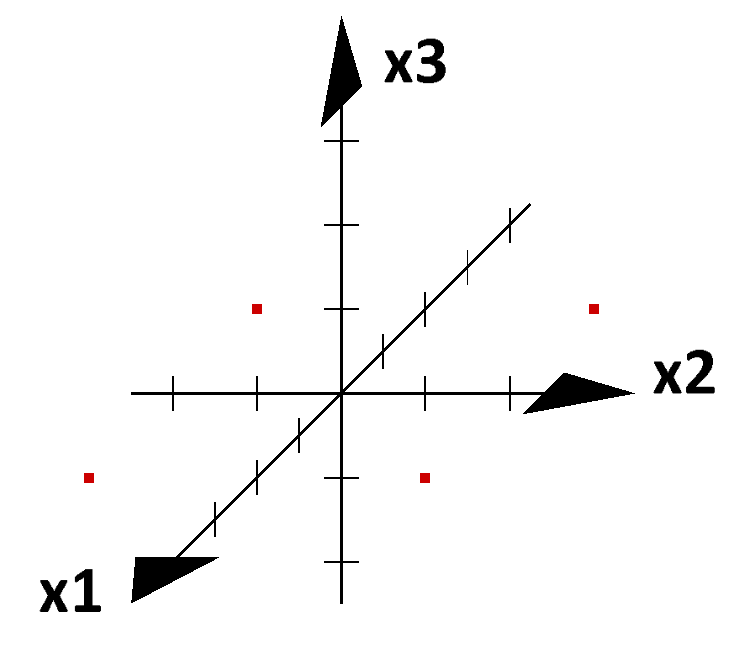
- Zeichnen Sie das Rechteck mit den Eckpunkten
$P_0(0\mid 0\mid 0)$,
$P_1(0\mid 3\mid 0)$,
$P_2(0\mid 3\mid 4)$ und
$P_3(0\mid 0\mid 4)$ in ein passendes Koordinatensystem ein.
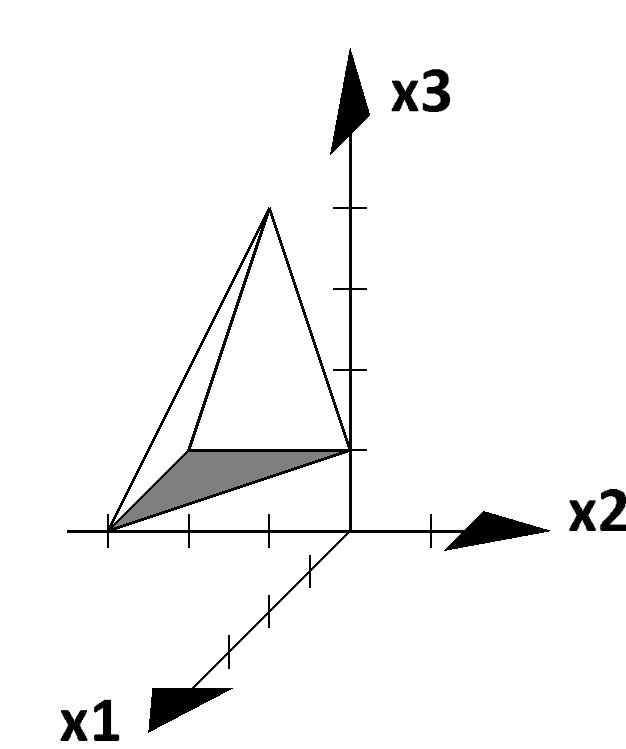
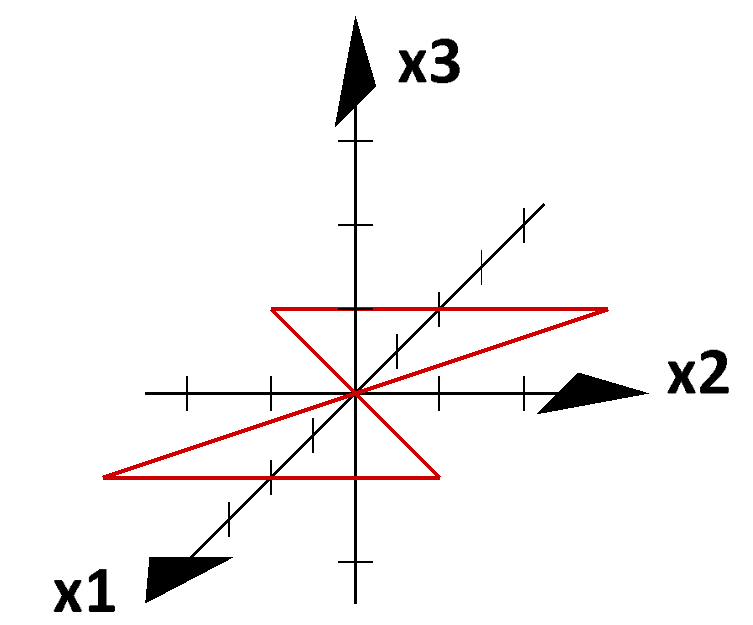
- Die Grundfläche einer Pyramide hat die Eckpunkte
$A(0\mid 0\mid 1)$,
$B(0\mid -2\mid 1)$ und
$C(2\mid -2\mid 1)$.
Die Spitze liegt bei $S(0\mid -1\mid 4)$.
Zeichnen Sie die Pyramide in ein passendes Koordinatensystem ein.
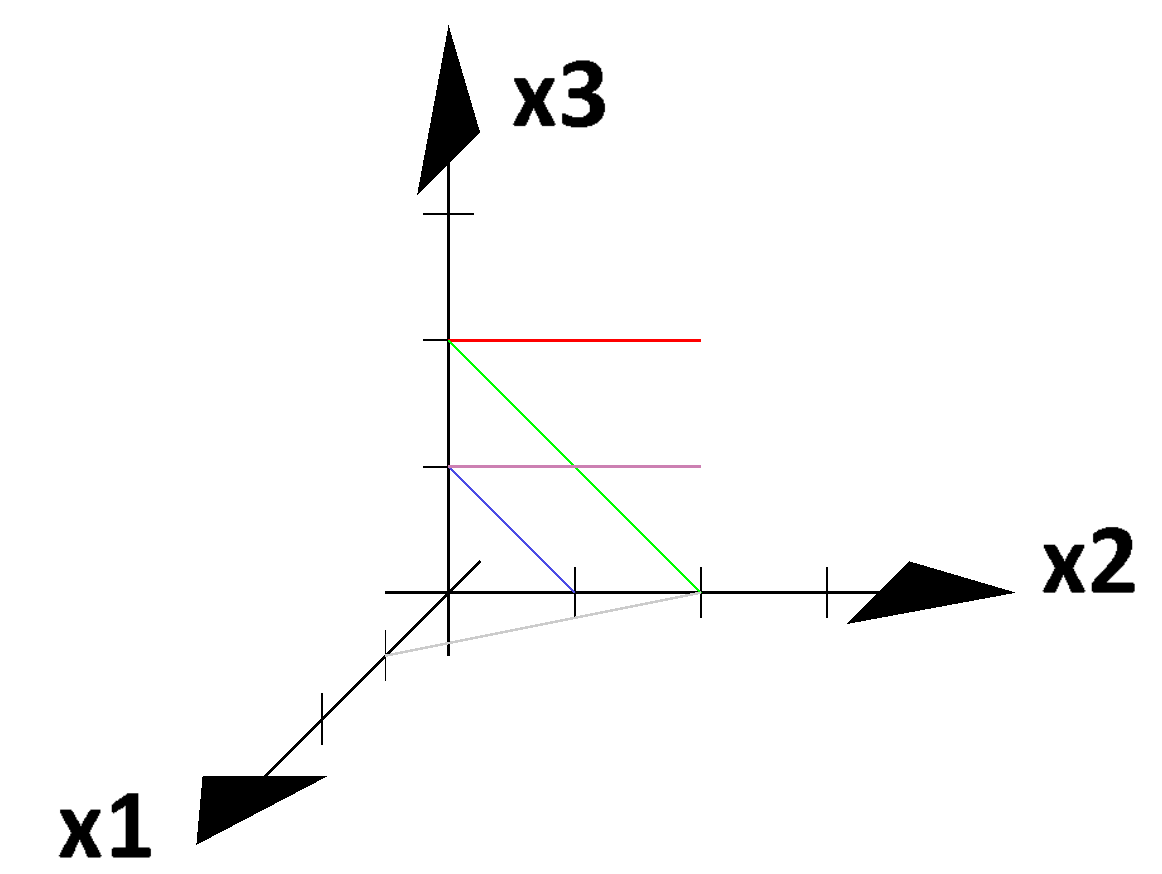
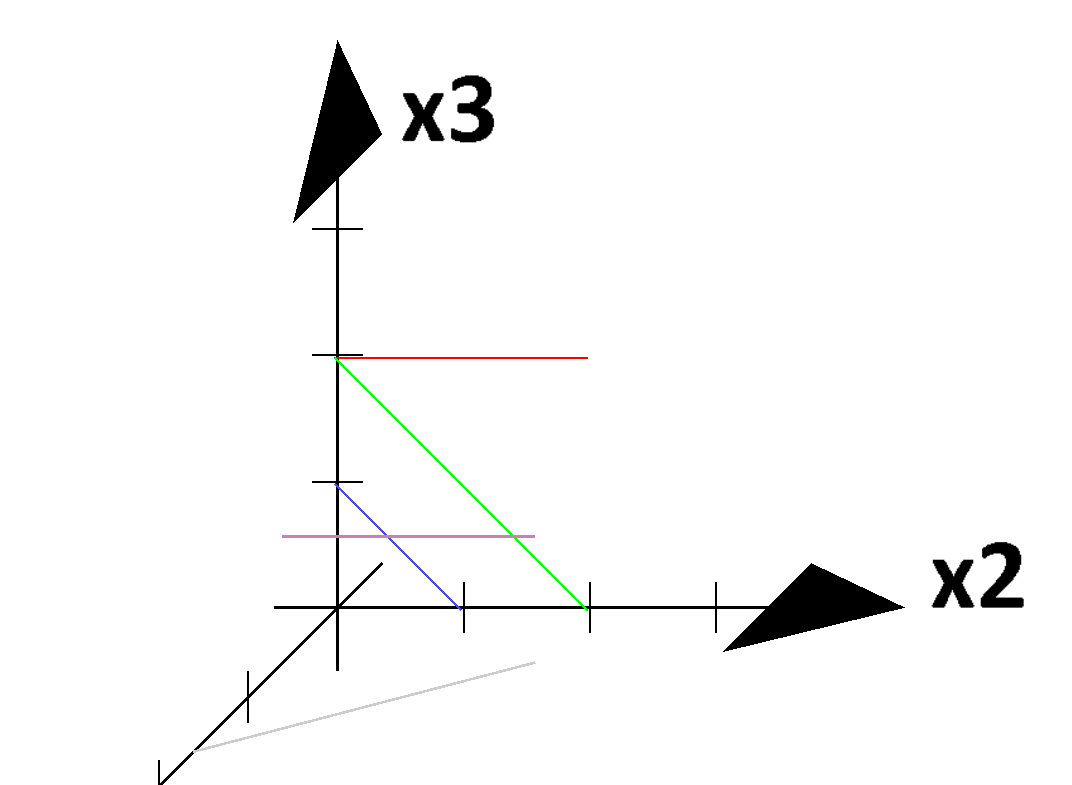
- Zeichnen Sie folgende Linien in ein Koordinatensystem ein:
Linie 1: von $(0\mid 0\mid 2)$ nach $(0\mid 2\mid 2)$
Linie 2: von $(0\mid 0\mid 2)$ nach $(0\mid 2\mid 0)$
Linie 3: von $(0\mid 0\mid 1)$ nach $(0\mid 1\mid 0)$
Linie 4: von $(2\mid 1\mid 2)$ nach $(2\mid 3\mid 2)$
Linie 5: von $(2\mid 3\mid 1)$ nach $(3\mid 1\mid 1)$
Welche Linien scheinen verbunden obwohl sie es nicht sind?
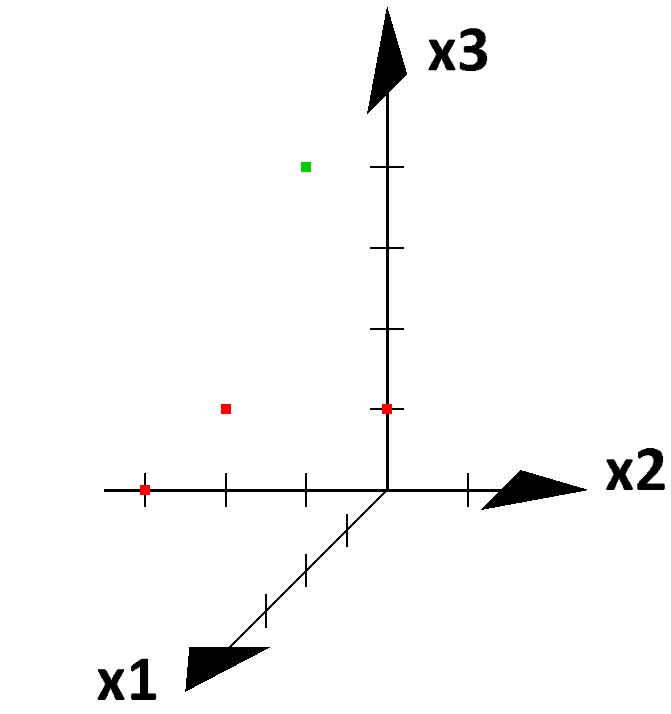
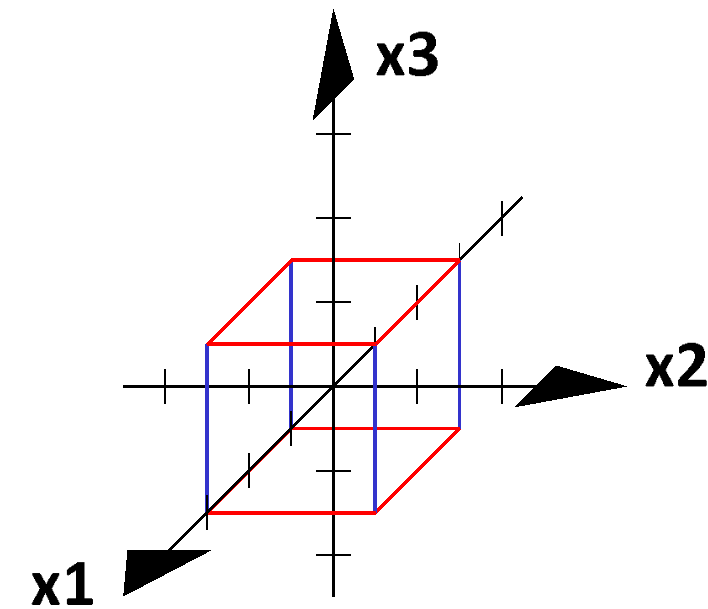
- Welche Eckpunkte hat ein Würfel mit Seitenlänge 2, bei dem der Ursprung in der Mitte liegt?
Ermitteln Sie die Punkte und zeichnen Sie den Würfel.