Gegeben ist der Punkt $A=\vz{0{,}5}{0{,}5}$.
Punkt $A$ wird mehrmals verschoben.
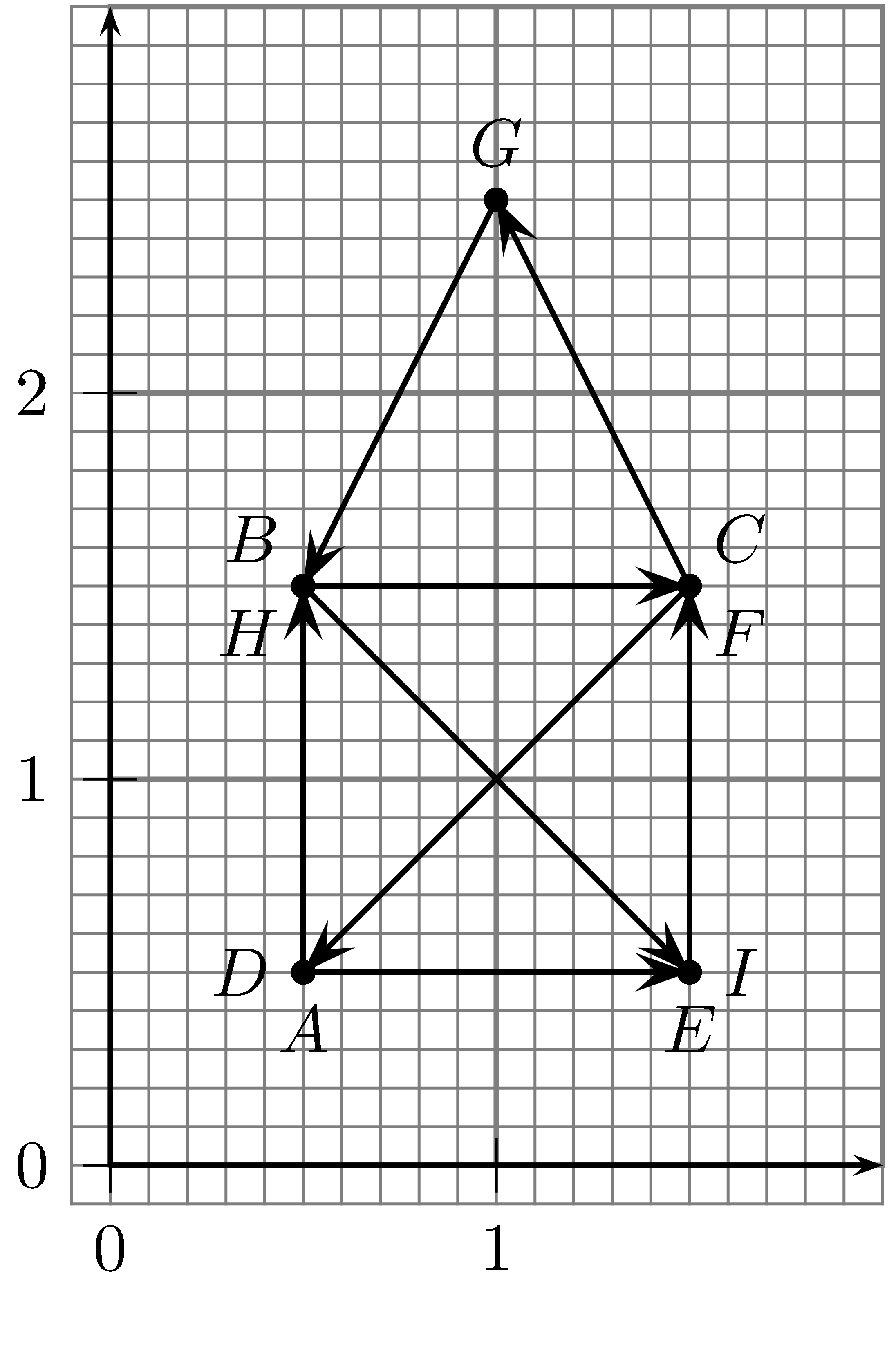
Zeichnen Sie jeden Verschiebungsvektor und den neuen Punkt ein. $B$ entsteht durch die Verschiebung von $A$ um den Vektor $\vec{v_0}=\vz{0}{1}$
$C$ entsteht durch die Verschiebung von $B$ um den Vektor $\vec{v_1}=\vz{1}{0}$
$D$ entsteht durch die Verschiebung von $C$ um den Vektor $\vec{v_2}=\vz{-1}{-1}$
$E$ entsteht durch die Verschiebung von $D$ um den Vektor $\vec{v_3}=\vz{1}{0}$
$F$ entsteht durch die Verschiebung von $E$ um den Vektor $\vec{v_4}=\vz{0}{1}$
$G$ entsteht durch die Verschiebung von $F$ um den Vektor $\vec{v_5}=\vz{-0{,}5}{1}$
$H$ entsteht durch die Verschiebung von $G$ um den Vektor $\vec{v_6}=\vz{-0{,}5}{-1}$
$I$ entsteht durch die Verschiebung von $H$ um den Vektor $\vec{v_7}=\vz{1}{-1}$
Zeichnen Sie jeden Verschiebungsvektor und den neuen Punkt ein. $B$ entsteht durch die Verschiebung von $A$ um den Vektor $\vec{v_0}=\vz{0}{1}$
$C$ entsteht durch die Verschiebung von $B$ um den Vektor $\vec{v_1}=\vz{1}{0}$
$D$ entsteht durch die Verschiebung von $C$ um den Vektor $\vec{v_2}=\vz{-1}{-1}$
$E$ entsteht durch die Verschiebung von $D$ um den Vektor $\vec{v_3}=\vz{1}{0}$
$F$ entsteht durch die Verschiebung von $E$ um den Vektor $\vec{v_4}=\vz{0}{1}$
$G$ entsteht durch die Verschiebung von $F$ um den Vektor $\vec{v_5}=\vz{-0{,}5}{1}$
$H$ entsteht durch die Verschiebung von $G$ um den Vektor $\vec{v_6}=\vz{-0{,}5}{-1}$
$I$ entsteht durch die Verschiebung von $H$ um den Vektor $\vec{v_7}=\vz{1}{-1}$
- Zeichnen Sie alle Punkte ein.
- Welche Punkte sind identisch?
- Welche Vektoren zeigen in die selbe Richtung?
- Finde Paare von Vektoren, welche in die entgegengesetzte Richtung zeigen.
- Welche Vektoren sind senkrecht zueinander?