Impressum
< Index

Graphisches Ableiten

Beim graphischen Ableiten ermittelt man die Steigung einer Funktion in einem Punkt.
Die Steigung der Funktion ist in einem Punkt genau so groß, wie die Steigung einer Tangente in diesem Punkt.
Zeichnet man eine Tangente an den Graph der Funktion und liest die Steigung der Tangente ab, so hat man auch die Steigung der Funktion in diesem Punkt.
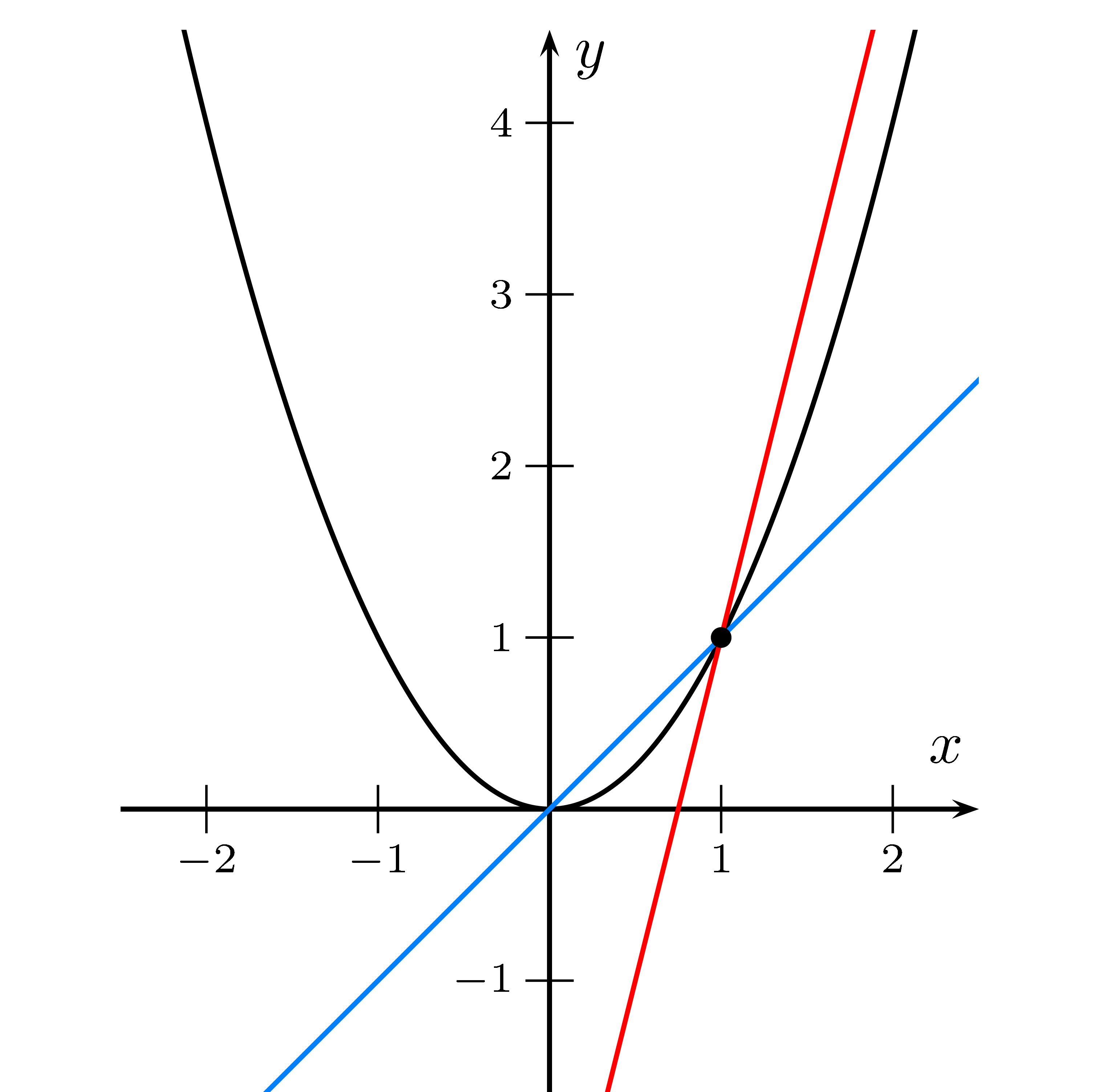
Im Schaubild $K_f$ von $f(x)=x^2$ sieht man zwei Sekanten durch den Punkt $P(1\mid 1)$. Die rote Sekante ist steiler als $K_f$ in $P$, da sie von unten nach oben durch $K_f$ geht.
Die blaue Sekante ist flacher, da sie von oben nach unten durch $K_f$ geht.
Das heißt es muss eine Tangente an $K_f$ in $P$ geben, deren Steigung zwischen der roten und der blauen Geraden liegt.
Legt man ein Geodreieck an $P$ an und dreht es so lange bis es eine Tangente darstellt und zeichnet diese ein, so kann man von der Tangente die Steigung ablesen.
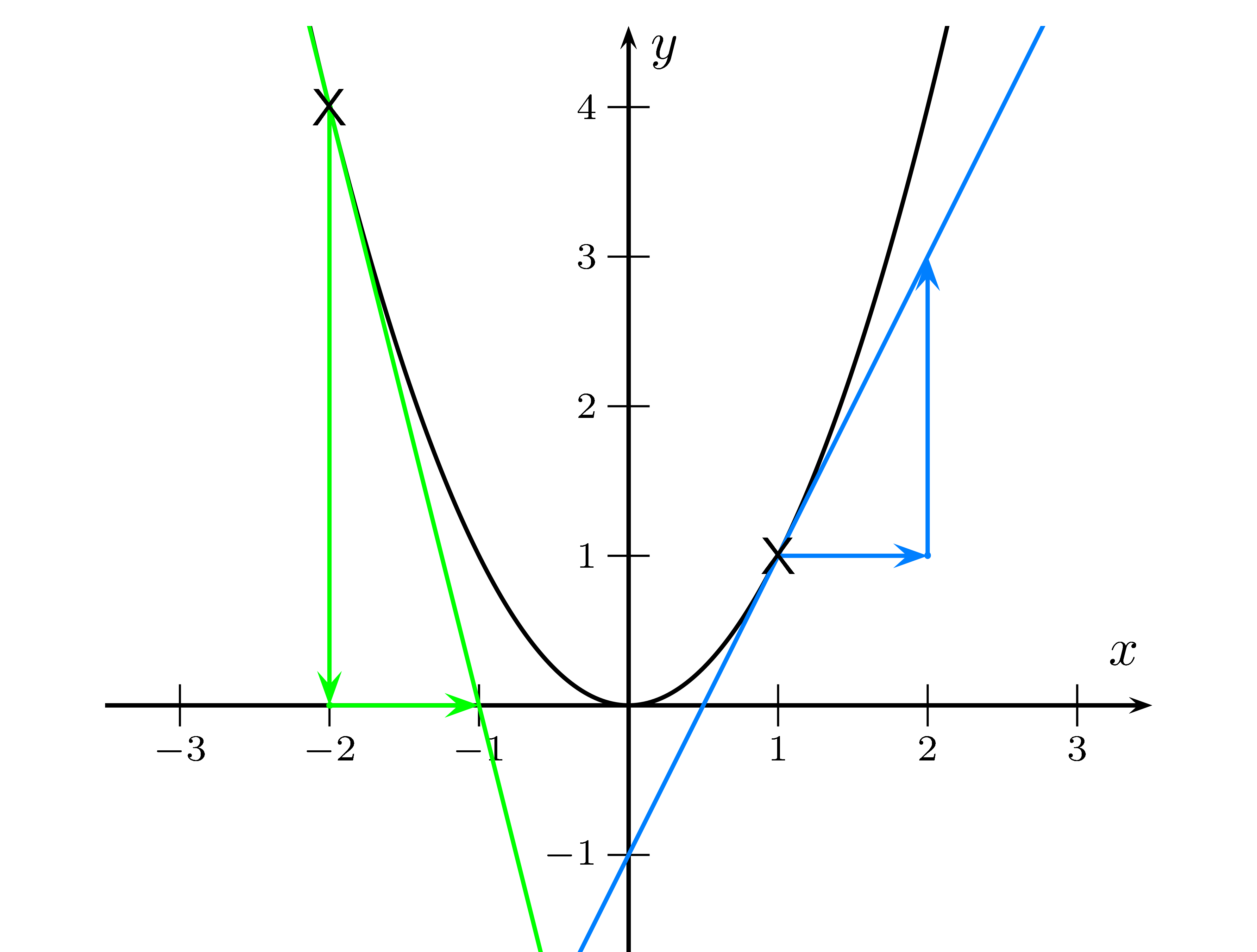
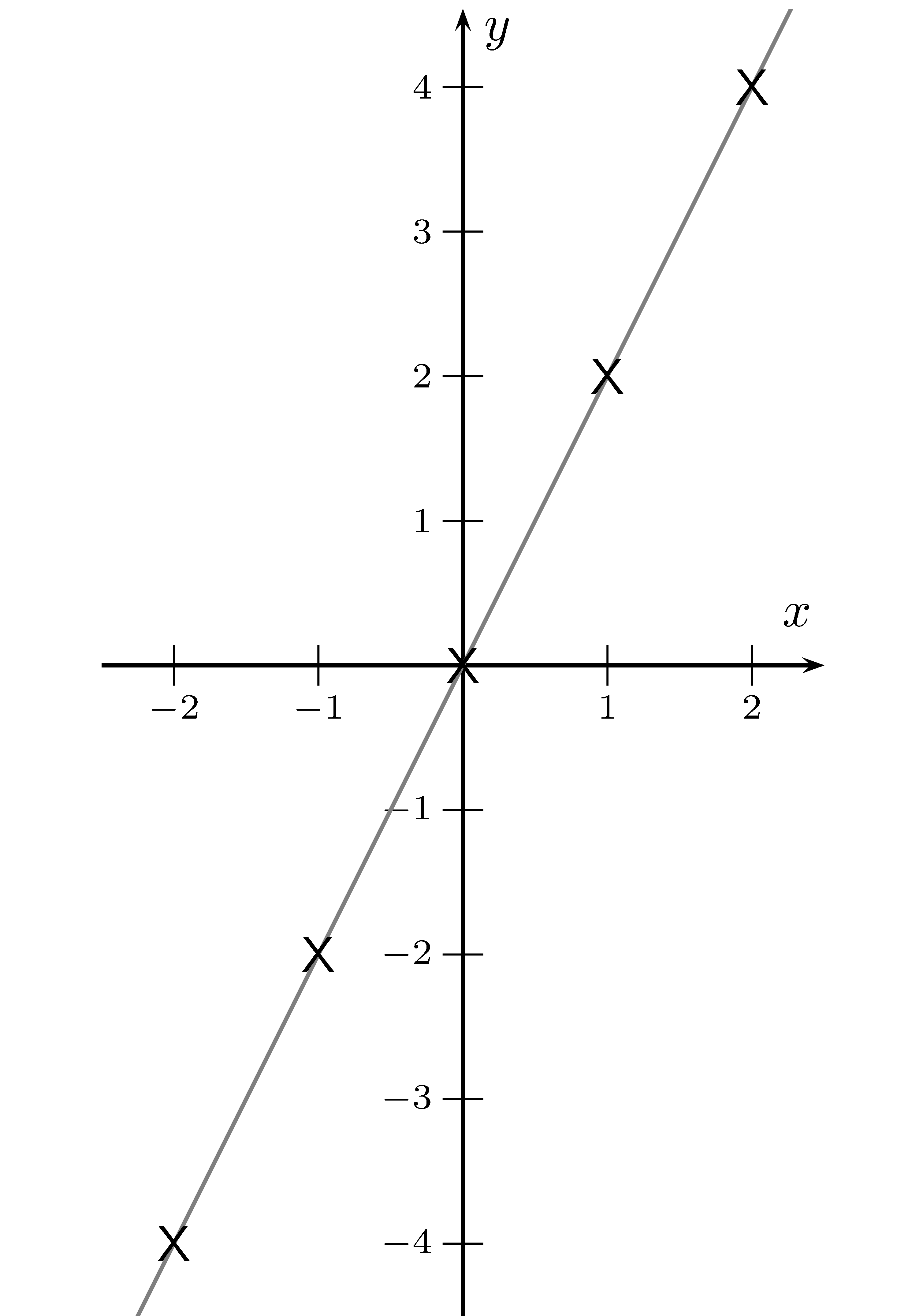
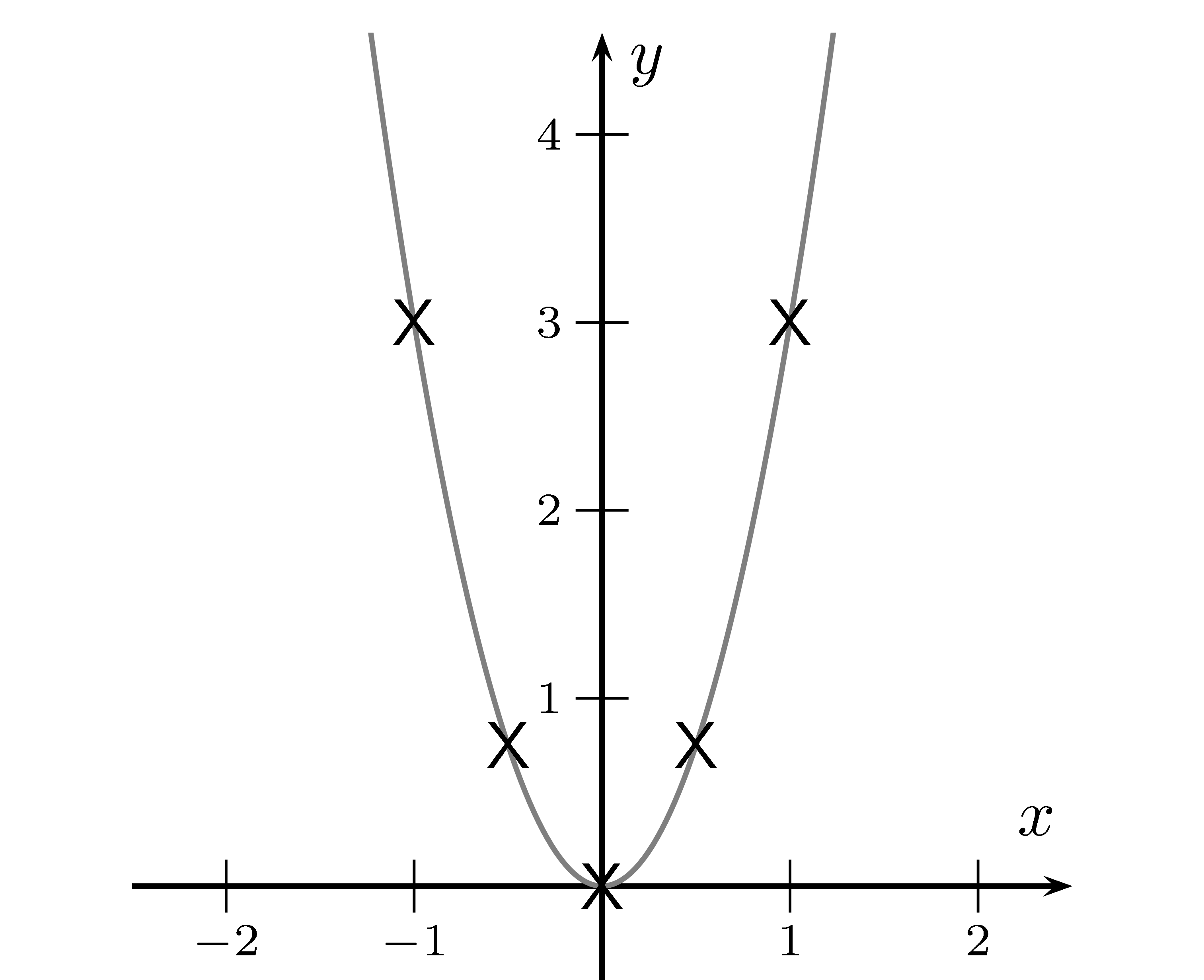
Im zweiten Schaubild sind zwei Tangenten an die Normalparabel eingezeichnet. Mithilfe der Steigungsdreiecke kann man für die grüne Tangente $m=-4$ ablesen, dies ist die Steigung von $f(x)=x^2$ bei $x=-2$.
Die blaue Tangente berührt bei $(1\mid 1)$. Hier ist die Steigung $m=1$, d.h. die Normalparabel hat bie $x=1$ eine Steigung von $1$.
Normalparabel mit 2 Geraden durch (1|1), die rote ist steil, die blaue flach
Die rote Gerade ist steiler als
$x^2$ bei $(1\mid 1)$, die grüne ist flacher.
Normalparabel mit 2 Tangenten an P(1|1) und Q(-2|4)
Normalparabel mit zwei eingezeichneten Tangenten

Graph der Ableitungsfunktion

Bestimmen wir von einem Funktionsgraphen mehrere Steigungswerte und tragen diese in ein neues Achsenkreuz ein, so können wir diese verbinden und erhalten das Schaubild der Ableitung.
Die Ableitung einer Funktion $f(x)$ gibt ihre Steigung an und wird als $f'(x)$ bezeichnet.
Beispiel 1: Bestimme die Steigungen der Tangenten an $f(x)=x^2$ für $x=-2; -1; 0; 1; 2$.
Ergebnis:
Die Tangenten haben die Steigungen: $-4; -2; 0; 2; 4$
Trägt man für jeden $x$-Wert die Steigung in ein Koordinatensystem ein, so liegen all diese Punkte auf einer Geraden (s. Schaubild).
Verbindet man diese Punkte erhält man die Gerade $y=2x$.
Somit ist die Ableitung von $f(x)=x^2$ die Funktion $f'(x)=2x$.
Beispiel 2: Bestimme die Steigungen der Tangenten an $f(x)=x^3$ für $x=-1; -0{,}5; 0; 0{,}5; 1$.
Ergebnis:
Die Tangenten haben die Steigungen: $3; 0{,}75; 0; 0{,}75; 3$
Trägt man für jeden $x$-Wert die Steigung in ein Koordinatensystem ein, so liegen Punkte auf einer Parabel (s. Schaubild).
Diese Parabel hat die Gleichung $y=3x^2$.
Somit ist die Ableitung von $f(x)=x^3$ die Funktion $f'(x)=3x^2$.
Die Ableitung der Normalparabel als Gerade y=2 mal x
Die Ableitung von $f(x)=x^2$ ist $f'(x)=2x$
Ableitung von x hoch 3 ist 3 mal x hoch 2
Die Ableitung von $f(x)=x^3$ ist $f'(x)=3x^2$