< Index

Die Steigung von Geraden

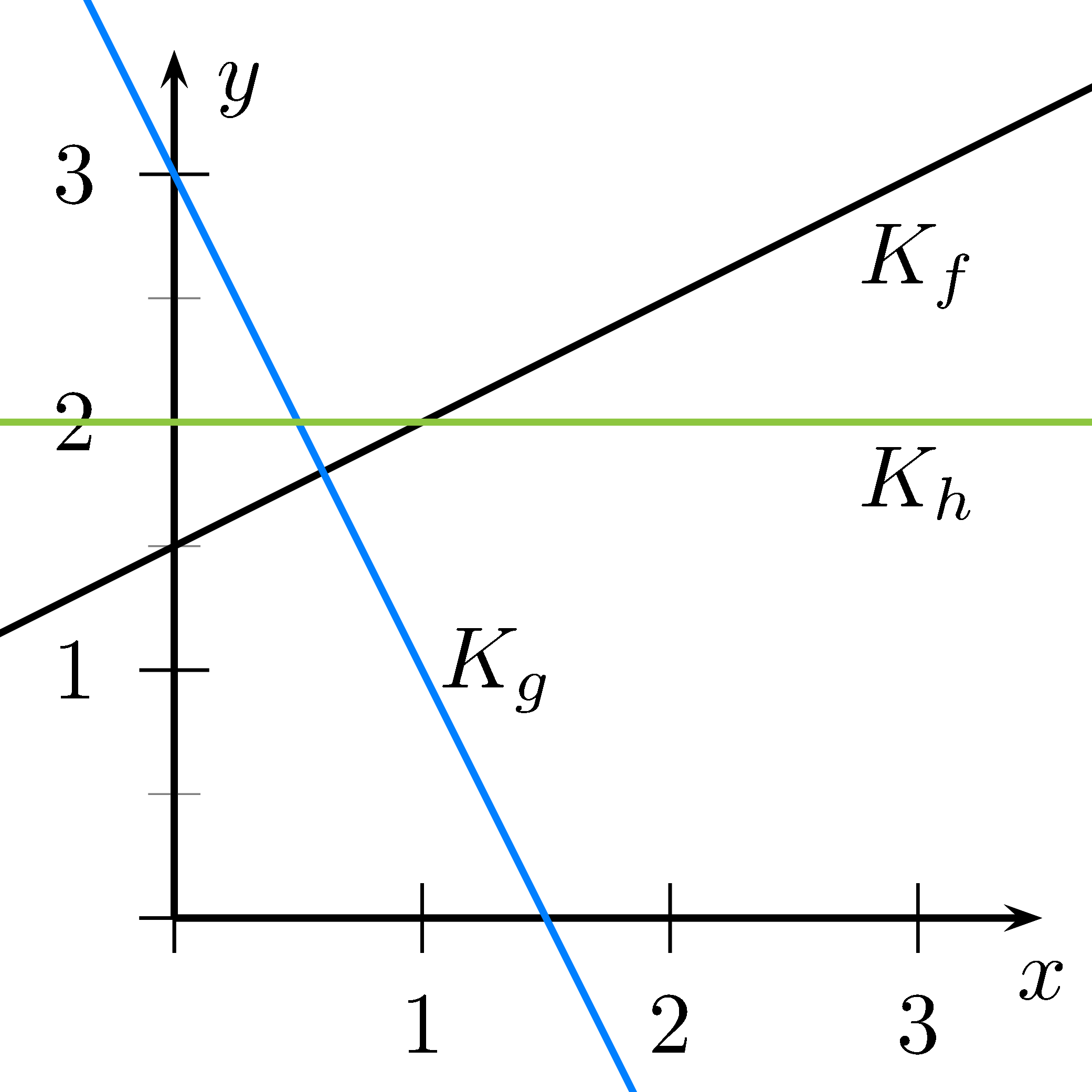
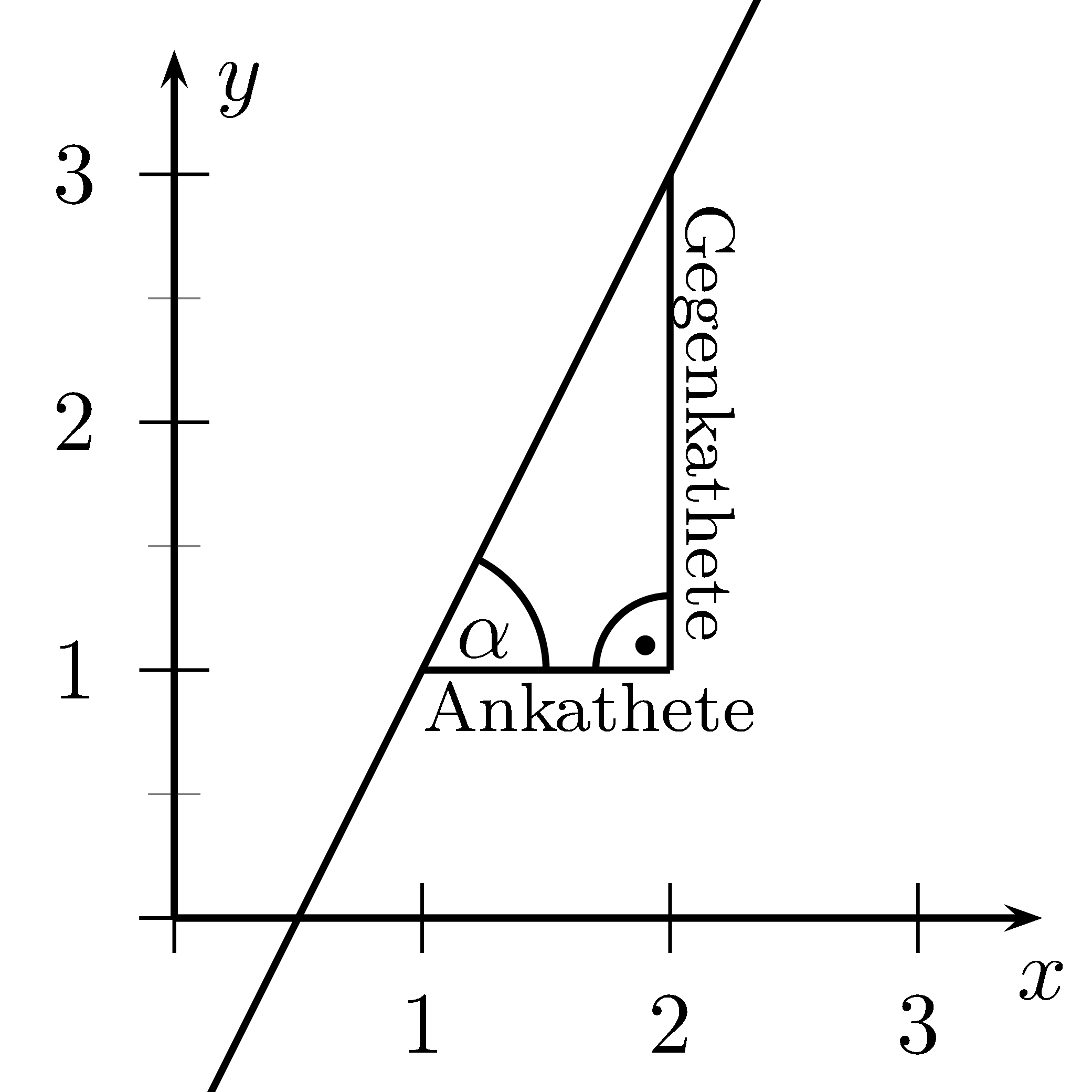
Die Steigung des Graphen einer linearen Funktion $f(x)=mx+b$ ist $m$.

Ist $m\lt 0$ so fällt die Gerade
Ist $m> 0$ so steigt die Gerade
Ist $m=0$ so ist die Gerade waagerecht

Bsp.:

Die Gerade von $f(x)=3x-10$ steigt, da die Steigung 3>0 ist.
Das Schaubild von $t(x)=-4x+2$ ist eine fallende Gerade, da die Steigung -4<0 ist.
Der Graph von $w(x)=\frac12x$ ist eine steigende Gerade, da $\frac12$>0
Die Gerade von $s(x)=0x+2$, also von $s(x)=2$ ist waagerecht.
Das Schaubild von $r(x)=-x+2$ ist eine fallende Gerade, da die Steigung -1 ist.

3 Geraden, je eine mit positiver, negativer und null Steigung — $K_f$ hat eine positive Steigung
$K_h$ hat die Steigung 0
$K_g$ hat eine negative Steigung

Aufgepasst: Bei waagerechten Geraden ist die Funktionsgleichung $f(x)=b$, da $m=0$ ist, kann man den Term $0\cdot x$ weglassen, weil er 0 ist und eine 0 bei einer Summe nichts verändert.
Das heißt $f(x)=4$, $g(x)=-2$ und $h(x)=0$ haben alle die Steigung 0. Man könnte sie ja so schreiben $f(x)=0x+4$, $g(x)=0x-2$ und $h(x)=0x+0$.

Steigungswinkel

Der Steigungswinkel der Geraden hängt mit $m$ wie folgt zusammen: $\tan(\alpha) = m$.
Mit der Umkehrfunktion des Tanges erhält man aus $m$ den Steigungswinkel $\alpha$: $\alpha=\tan^{-1}(m)$ oder $\alpha=\arctan(m)$.
Die Umkehrfunktion erhält man bei den meisten Taschenrechnern mit shift+tan oder second+tan.

$\alpha$ ist positiv, wenn die Gerade steigt
$\alpha$ ist negativ, wenn die Gerade fällt
$\alpha$ ist 0, wenn die Gerade waagerecht ist

$\alpha=\frac{\text{Gegenkathete}}{\text{Ankathete}}=\tan^{-1}(m)$

Bsp:

Steigungswinkel von $f(x)=2x+1$
$\begin{array}{rcl} \tan(\alpha) &=& 2\\ \alpha &=& \tan^{-1}(2)\\ \alpha &=& 63{,}43^\circ\\ \end{array}$
Steigungswinkel von $g(x)=\frac12x-2$
$\begin{array}{rcl} \tan(\alpha) &=& \frac12\\ \alpha &=& \tan^{-1}\left(\frac12\right)\\ \alpha &=& 26{,}57^\circ\\ \end{array}$
Steigungswinkel von $g(x)=-x-4$ (d.h. $m=-1$)
$\begin{array}{rcl} \tan(\alpha) &=& -1\\ \alpha &=& \tan^{-1}\left(-1\right)\\ \alpha &=& -45^\circ\\ \end{array}$