< Index

Strecken in $x$-Richtung

Um eine Funktion $f$ um $a$ in $x$-Richtung zu strecken ersetzt man jedes $x$ durch $\frac1a$.

Ist $a\gt 1$ so wird das Schaubild von $f$ gestreckt (in die Länge gezogen).
Ist $0\lt a \lt 1$ so wird das Schaubild von $f$ gestaucht (zusammengedrückt).
Ist $a\lt 0$ so wird $f$ zusätzlich an der $y$-Achse gespiegelt.

Diese Streckung funktioniert bei allen Funktionen, also Polynomen, Wurzelfunktionen, Exponential-Funktionen, trigonometrischen Funktionen, ...
Eben bei allen.

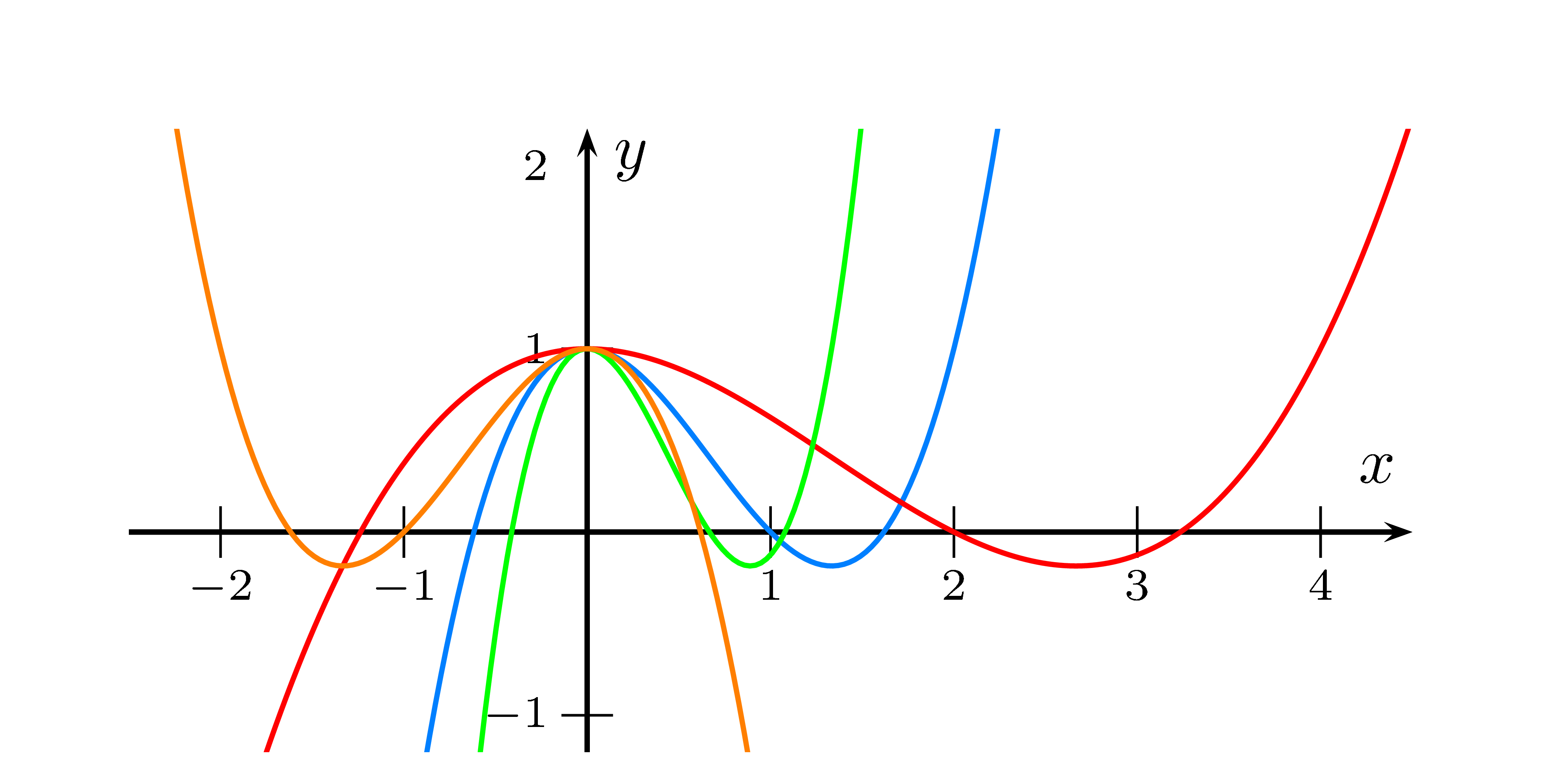
Schaubilder von x hoch 3 minus 2 mal x hoch 2 plus 1 und
dasselbe um 0,5 gestreckt und um 1,5 gestaucht und um -1, also gespiegelt — blau ist $f(x)=x^3-2x^2+1$
rot ist $f$ um 2 gestreckt, also $g(x)=\left(\frac12x\right)^3-2\left(\frac12x\right)^2+1$
grün ist $f$ mit $\frac23$ gestaucht , also $g(x)=\left(\dfrac1{\frac23}x\right)^3-2\left(\dfrac1{{\frac23}}x\right)^2+1$
orange ist $f$ um -1 gesteckt (also gespiegelt) $f(x)=(-1x)^3-2(-1x)^2+1$