Impressum
< Index

Parabeln in Scheitelform aufstellen/ablesen

Wenn die Funktionsgleichung einer Parabel gesucht ist und der Scheitelpunkt $S$ und ein weiterer Punkt $P$ gegeben sind, dann ist der beste Ansatz die Scheitelform der Parabel zu verwenden.
  1. Scheitelform $y=a(x-x_s)^2+y_s$ verwenden
  2. $x_s$ und $y_s$ aus dem Scheitelpunkt $S(x_s\mid y_s)$ einsetzen
  3. $x$ und $y$ aus dem Punkt $P(x\mid y)$ einsetzen
  4. jetzt kann man $a$ berechnen
  5. fertig
Bsp.:
  1. Geg.: Scheitel $S(3\mid 4)$ und der Punkt $P(1\mid 2)$
    Ges.: Die Gleichung der Parabel mit Scheitel $S$, die durch $P$ geht.
    Lösung:
    Ansatz: $y=a(x-x_s)^2+y_s$
    $S$ einsetzen: $y=a(x-3)^2+4$
    $P$ einsetzen: $2=a(1-3)^2+4$
    $a$ berechnen:
    $\begin{array}{rcll} 2&=&a(1-3)^2+4 & | \text{ zusammenfassen}\\ 2&=&a(-2)^2+4 & | \text{ zusammenfassen}\\ 2&=&4a+4 & | -4\\ -2&=&4a & | :4\\ -\frac12 &=& a \end{array}$
    Einsetzen von $a$, $x_s$ und $y_s$:
    $f(x)=-\frac12(x-3)^2+4$
    fertig
  2. Geg.: Scheitel $S(0\mid -2)$ und der Punkt $P(-1\mid -1)$
    Ges.: Die Gleichung der Parabel mit Scheitel $S$, die durch $P$ geht.
    Lösung:
    Ansatz: $y=a(x-x_s)^2+y_s$
    $S$ einsetzen: $y=a( x-0)^2+(-2)$
    $P$ einsetzen: $-1=a(-1-0)^2+(-2)$
    $a$ berechnen:
    $\begin{array}{rcll} -1&=&a(-1-0)^2+(-2) & | \text{ zusammenfassen}\\ -1&=&a(-1)^2-2 &\\ -1&=&a-2 & | +2\\ 1&=&a & \end{array}$
    Einsetzen von $a$, $x_s$ und $y_s$:
    $f(x)=(x-0)^2-2$ oder $f(x)=x^2-2$
    fertig

Parabel vom Schaubild ablesen

Manchmal ist das Schaubild der Parabel gegeben und man soll die Funktionsgleichung ermitteln.
Wenn in dem Schaubild der Scheitel und ein weiterer Punkt gut ablesbar sind, dann ist die Scheitelform der Funktionsgleichung am schnellsten erstellt.
  1. Scheitel ablesen
  2. Punkt ablesen
  3. weiter wie oben
Bsp.:
  1. Geg.: Das Schaubild
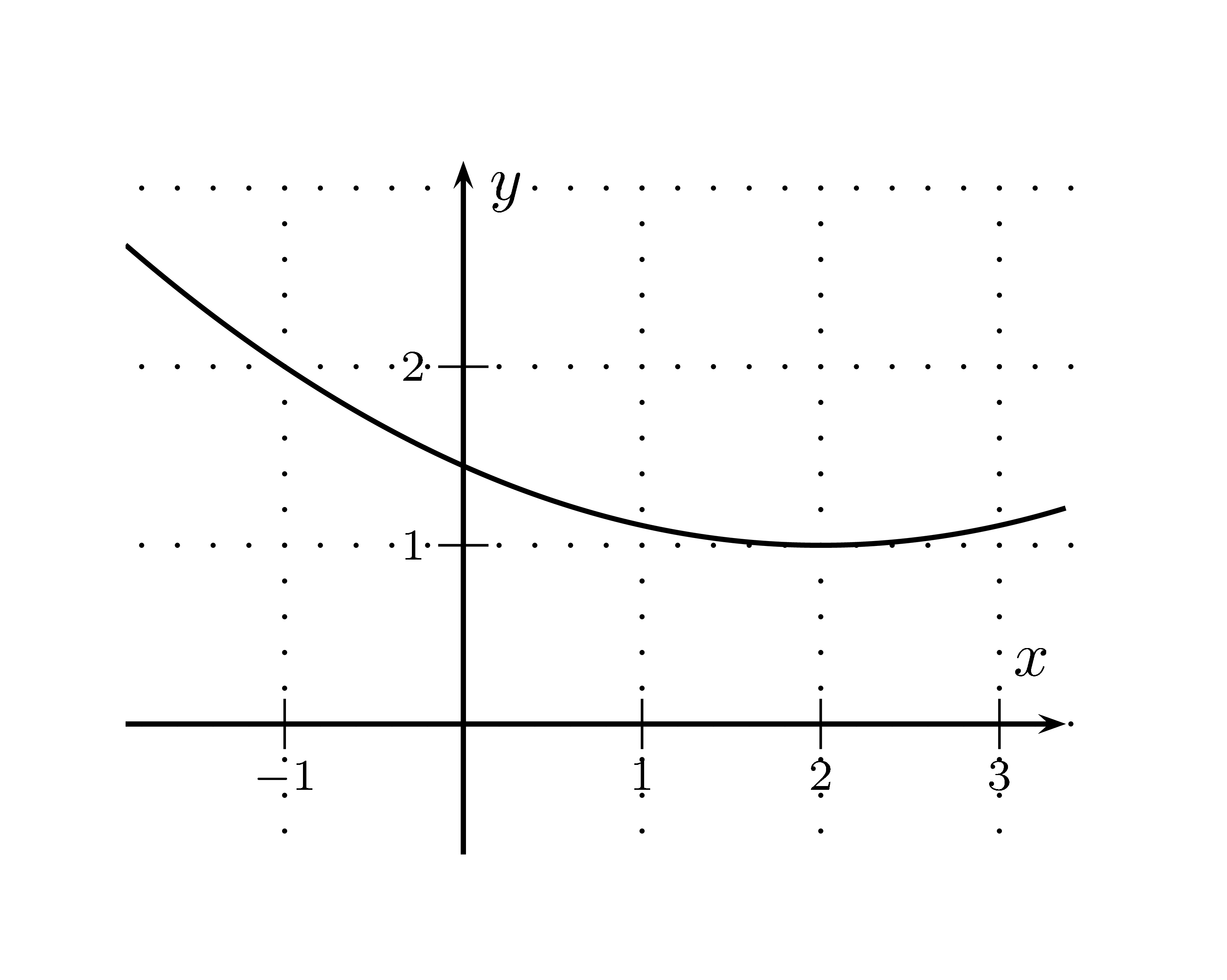
    Parabel mit Scheitel bei (2|1) und P(-1|2)
    Ges.: Die Funktionsgleichung der Parabel.
    Lösung: Scheitel ablesen: $S(2\mid 1)$; Punkt ablesen: $P(-1\mid 2)$
    Ansatz: $y=a(x-x_s)^2+y_s$
    $S$ und $P$ einsetzen: $2=a( -1-2)^2+1$
    $a$ berechnen:
    $\begin{array}{rcll} 2&=&a(-1-2)^2+1 & | \text{ zusammenfassen}\\ 2&=&9a+1 & | -1\\ 1&=&9a & | :9\\ \frac19&=&a & \end{array}$
    Einsetzen von $a$, $x_s$ und $y_s$:
    $f(x)=\frac19(x-2)^2+1$
    fertig
  2. Geg.: Das Schaubild
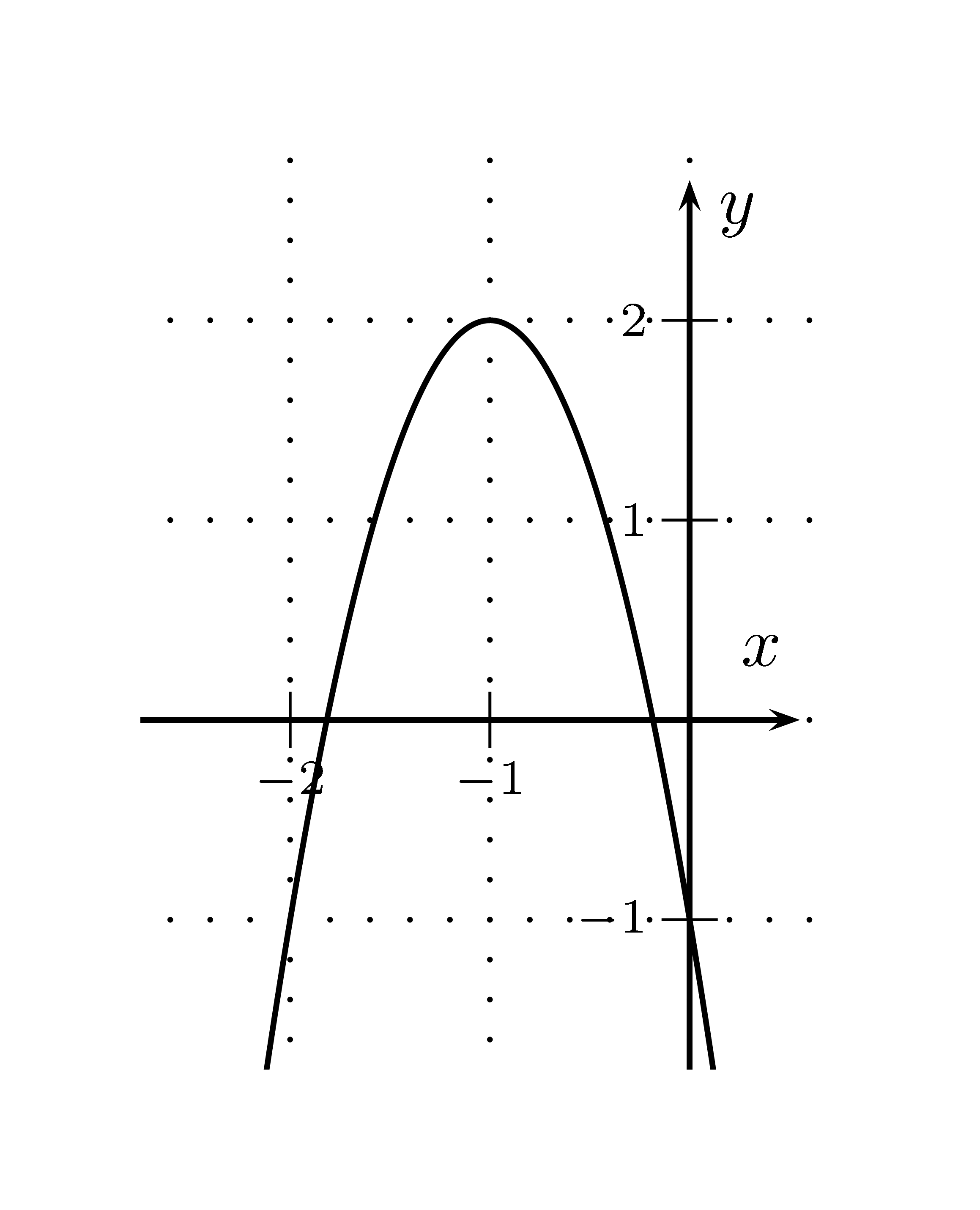
    Parabel mit Scheitel bei (-1|2) und P(0|-1)
    Ges.: Die Funktionsgleichung der Parabel.
    Lösung: Scheitel ablesen: $S(-1\mid 2)$; Punkt ablesen: $P(0\mid -1)$
    Ansatz: $y=a(x-x_s)^2+y_s$
    $S$ und $P$ einsetzen: $-1=a( 0-(-1))^2+2$
    $a$ berechnen:
    $\begin{array}{rcll} -1&=&a( 0-(-1))^2+2 & | \text{ zusammenfassen}\\ -1&=&1a+2 & | -2\\ -3&=&a & \\ \end{array}$
    Einsetzen von $a$, $x_s$ und $y_s$:
    $f(x)=-3(x+1)^2+2$
    fertig