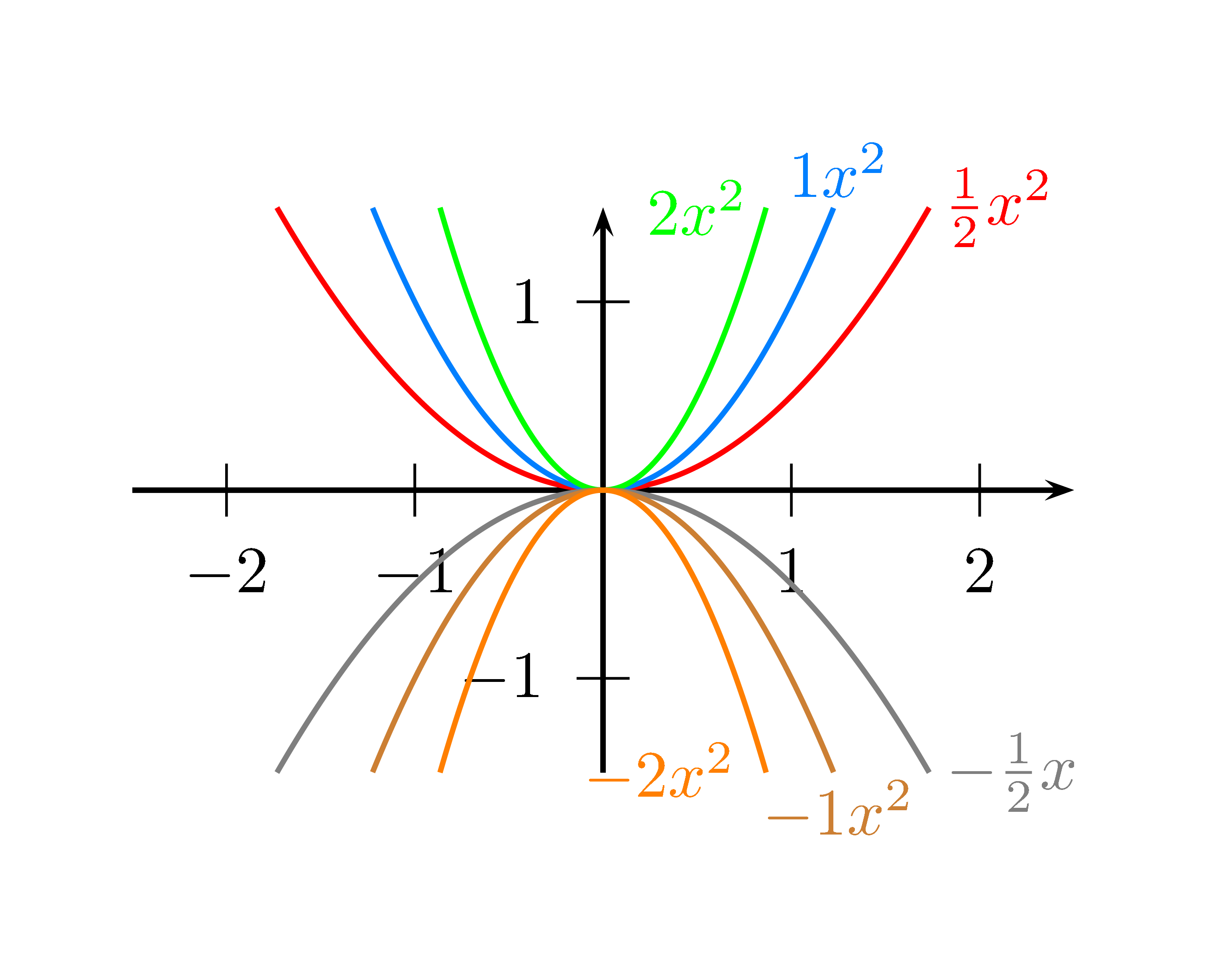
- Normalform: $f(x)=ax^2+bx+c$
- Scheitelform:
$f(x)=a\left(x-x_s\right)^2+y_s$
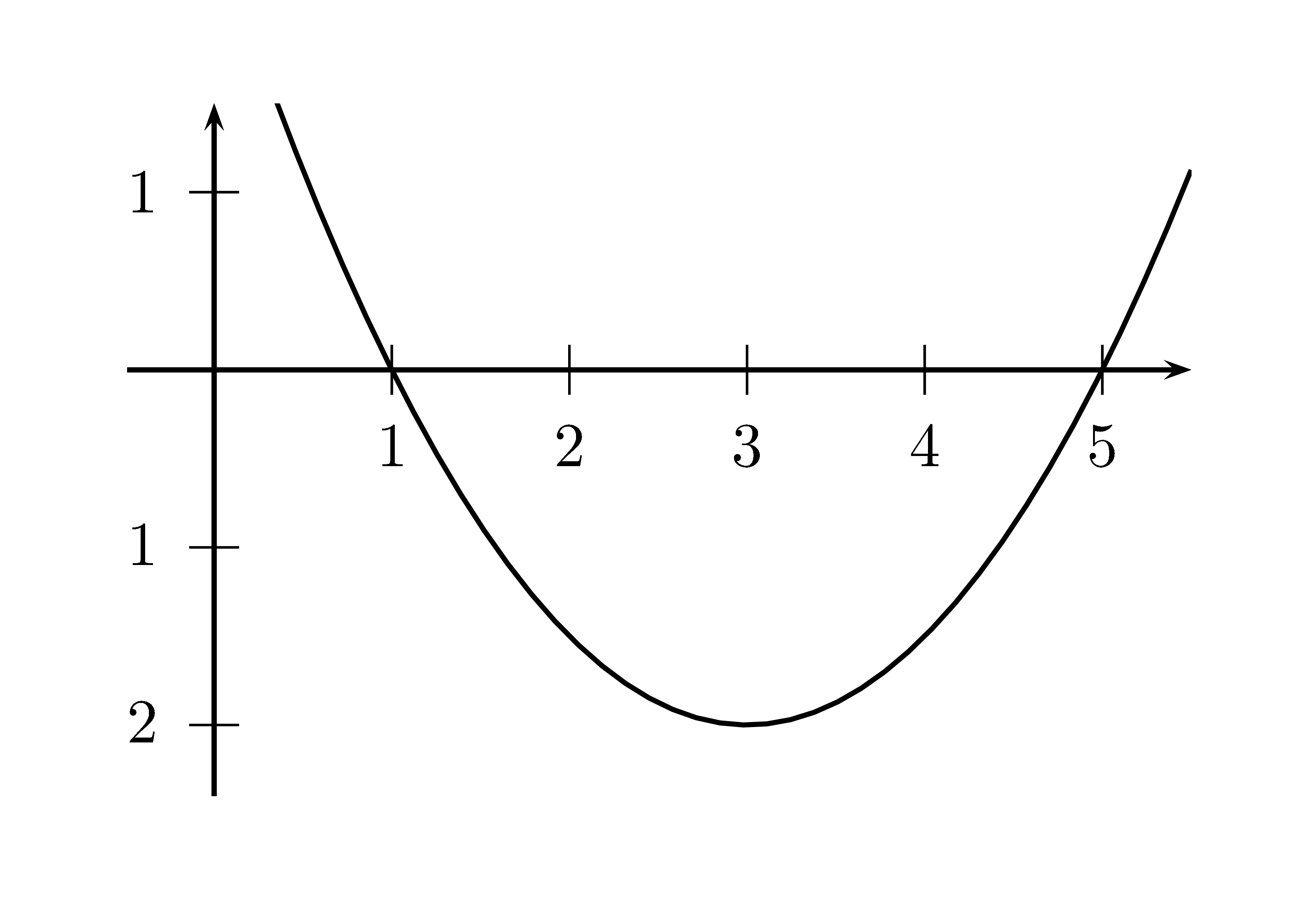
Die Werte von $x_s$ und $y_s$ sind die Koordinaten des Scheitelpunkts der Parabel: $S(x_s\mid y_s)$ - Produktform:
$f(x)=a\left(x-n_1\right)\left(x-n_2\right)$
Die Werte von $n_1$ und $n_2$ sind die Nullstellen der Parabel. Es erschließt sich, wenn man an den Satz vom Nullprodukt denkt.
Man kann jede Parabel in der Normalform und der Scheitelform angeben.
Eine Darstellung in Produktform ist nur möglich, wenn die Parabel zwei Nullstellen hat.