Funktionsbegriff

Definition: Eine Funktion ordnet jedem Wert einer Definitionsmenge genau einen Wert einer Wertemenge zu.

Hierbei bedeutet:

Definitionsmenge eine Sammlung von Dingen, dies kann alles sein, wie z.B. Tasten eines Automaten, unterschiedliche Süßigkeiten, ...
In der Analysis besteht die Definitionsmenge aus Zahlen.
ordnet zu heißt, dass es für jedes Element der Definitionsmenge ein Element der Wertemenge gibt.
genau ein bedeutet eins, nicht keins und nicht mehrere, sondern genau eins
Wertemenge ist die Sammlung aller zugeordneten Elemente.
Wenn jeder Süßigkeit ein Beliebtheitswert zugeordnet ist, dann ist die Menge der Beliebtheitswerte die Wertemenge.
Wenn jeder Zahl eine andere Zahl zugeordnet ist, dann sind diese Zahlen die Wertemenge.
Wenn jeder Zahl eine Farbe zugeordnet ist, dann bilden die Farben die Wertemenge.
Die Wertemenge umfasst aber nur die Elemente, die einem Element aus der Definitionsmenge zugeordnet wurden, sonst keins.
Das ist aber keine Einschränkung an sich, da man die Wertemenge ja verkleinern kann, bis nur noch solche Elemente in ihr enthalten sind.

Funktionsschreibweise

Mathematische Funktionen können auf unterschiedliche Weise dargestellt werden:

$\overbrace{f(x) = \underbrace{2x+1}_{\text{Funktionsterm}}}^{\text{Funktionsgleichung}}$ mit $x\in\mathbb{R}$
sprich: $f$ von $x$ ist gleich $2x+1$
Hier wird jedem $x$ ein Funktionswert $f(x)$ zugeordnet.
Der zuordnete Wert ergibt sich aus dem Funktionsterm $2x+1$.
Da $x\in\mathbb{R}$ gilt, darf man für $x$ jede reelle Zahl wählen.
$f$ ist der Name der Funktion und er kann frei gewählt werden.
Hier ein paar Beispiele für die Funktion $f(x)=2x+1$:
$x=0$ ist $1$ zugeordnet (da $2\cdot0+1=1$)
$x=-2$ ist $-3$ zugeordnet(da $2\cdot(-2)+1=-3$)
$x=5$ ist $11$ zugeordnet
$x=100$ ist $201$ zugeordnet
$f:\ x\mapsto 2x+1$ ist dieselbe Funktion. Den Pfeil $\mapsto$ liest man "wird zugeordnet".
Sprich: Die Funktion $f$ ordnet jedem $x$ den Wert $2x+1$ zu oder
Sprich: Die Funktion $f$ bildet $x$ auf $2x+1$ ab.
Man kann in dieser Schreibweise auch die Definitions- und Wertemenge mit einbauen:
$f:\ \mathbb{R}\rightarrow\mathbb{R},\ x\mapsto 2x+1$
Sprich: $f$ bildet von den reellen Zahlen in die reellen Zahlen ab und ordnet jedem $x$ den Wert von $2x+1$ zu.

In der Schule wird meist die erste Schreibweise verwendet.

Darstellungen von Funktionen

Wertetabelle
Da eine Funktion $x$-Werte auf Funktionswerte abbildet, kann man diese Abbildung in einer Tabelle darstellen. Man listet hier $x$-Werte und die zugehörigen Funktionswerte auf.
$\begin{array}{l||r|r|r|r|r|r|r|r|r|} \hline x & -4 & -3 & -2 & -1 & 0 & 1 & 2 & 3 & 4\\\hline f(x) & -7 & -5 & -3 & -1 & 1 & 3 & 5 & 7 & 9\\\hline \end{array}$
Vorteile:

Der Funktionswert kann direkt abgelesen werden
Die Punkte $(x\mid f(x))$ können direkt in ein Achsenkreuz eingezeichnet werden

Nachteile:

Für nicht enthaltene $x$-Werte kann man den Funktionswert nicht ermitteln.
Will man wissen, welcher Funktionswert zu $x=-10$ oder $x=0{,}5$ gehört, hilft die obige Wertetabelle nicht weiter.
Zeigt nicht die ganze Funktion, sondern nur einen Teil der Zuordnung
Wenn man nicht weiß, welcher Funktionstyp hinter der Wertetabelle steckt, kann man keinen Funktionsterm aus der Wertetabelle herleiten.

Graph
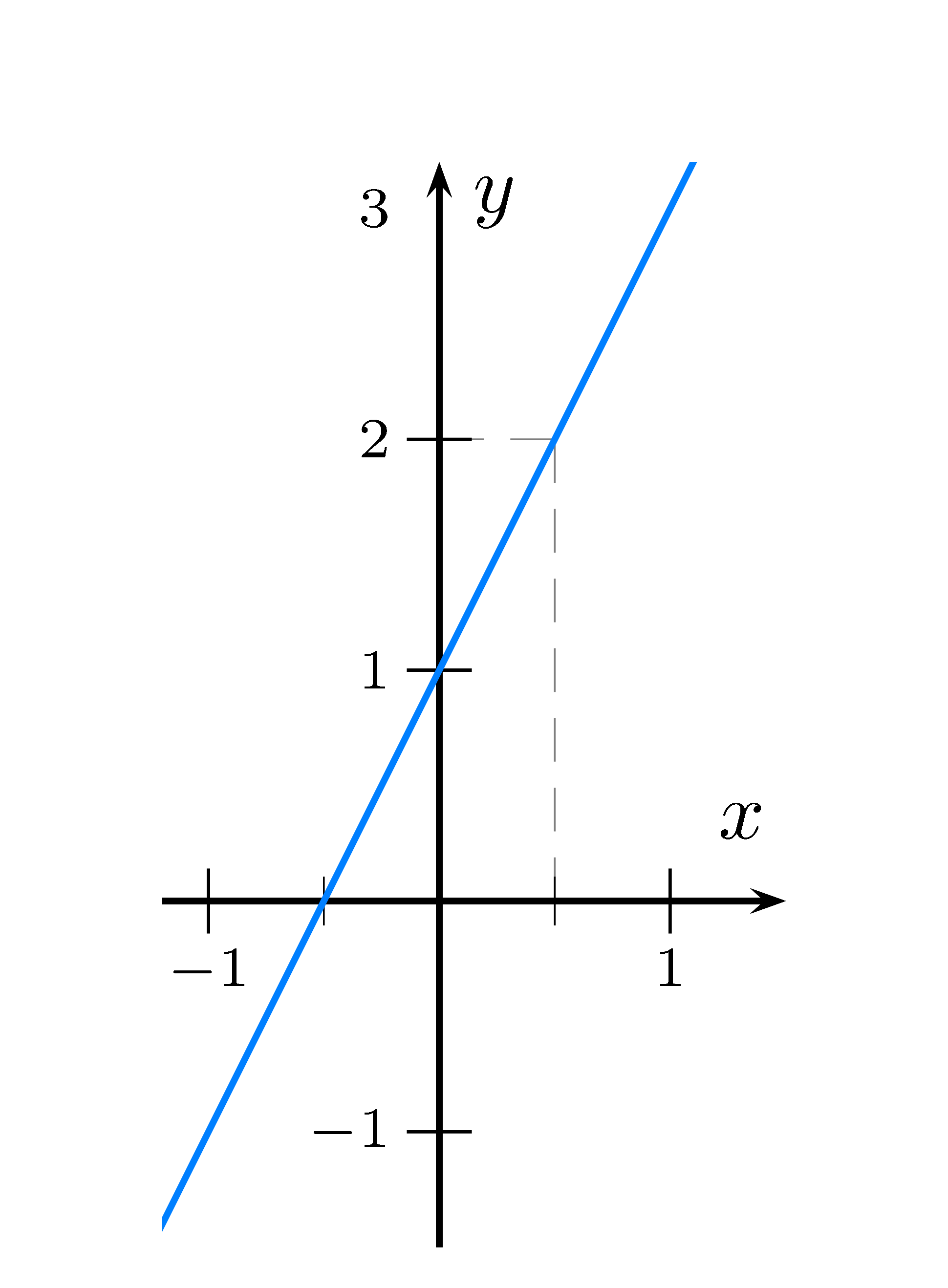
Der Graph (oder Schaubild) gibt die Abbildung der Funktion graphisch wieder.
Der $x$-Wert wird auf der waagerechten Achse abgetragen, der zugeordnete Funktionswert auf der senkrechten Achse.
Somit ist jeder Punkt $P$ auf dem Schaubild ein Paar von $x$ und $f(x)$ Werten.

Vorteile:

Der Funktionswert kann direkt abgelesen werden
Für jedes $x$ im Zeichenbereich kann man den Funktionswert ermitteln, indem man bis zum Schaubild senkrecht nach oben geht und dann waagerecht bis zur $y$-Achse.

Nachteile:

Zeichnungen sind immer ungenau.
Benötigt man den exakten Funktionswert auf mehrere Nachkommastellen genau, ist dies mit einem Schaubild nicht möglich.
Für nicht enthaltene $x$-Werte kann man den Funktionswert nicht ermitteln.
Will man wissen, welcher Funktionswert zu $x=-10$ oder $x=5$ gehört, hilft das obige Schaubild nicht weiter.
Wenn man nicht weiß, welcher Funktionstyp hinter dem Schaubild steckt, kann man keinen Funktionsterm aus ihm herleiten.

Funktionsgleichung
Eine Funktionsgleichung $f(x)=2x+1$ ermöglicht es für alle $x$ den Funktionswert zu berechnen.
Vorteile:

Der Funktionswert kann exakt berechnet werden.
Auch für "krumme" $x$ Werte wie $\sqrt{2}$ kann der Funktionswert bestimmt werden.
Der $x$-Bereich ist nicht beschränkt wie im Schaubild oder der Wertetabelle. Hier kann $f(x)$ für jedes $-\infty\lt x \lt \infty$ bestimmt werden.
Aus der Funktionsgleichung kann man leicht eine Wertetabelle oder ein Schaubild herleiten.

Nachteile:

Eine Funktionsgleichung ist abstrakt, d.h. man sieht hier den Verlauf nicht so gut, wie im Schaubild.
Diese abstrakte, also nicht anschauliche Darstellung, bereitet vielen Menschen anfänglich Probleme. Wenn man eine Reihe von Funktionen und ihre Gleichungen gesehen hat, fängt der Kopf an, die passenden Schaubilder zu den abstrakten Funktionstermen von selbst zu bilden.
Ab diesem Punkt ist man fit in Mathe. Bis dahin muss man durchhalten.

Will man exakt rechnen, so nimmt man die Funktionsgleichung.

Will man den Verlauf betrachten, so nimmt man den Funktionsgraphen.

Benötigt man einzelne Punkte, so entnimmt man sie der Wertetabelle.