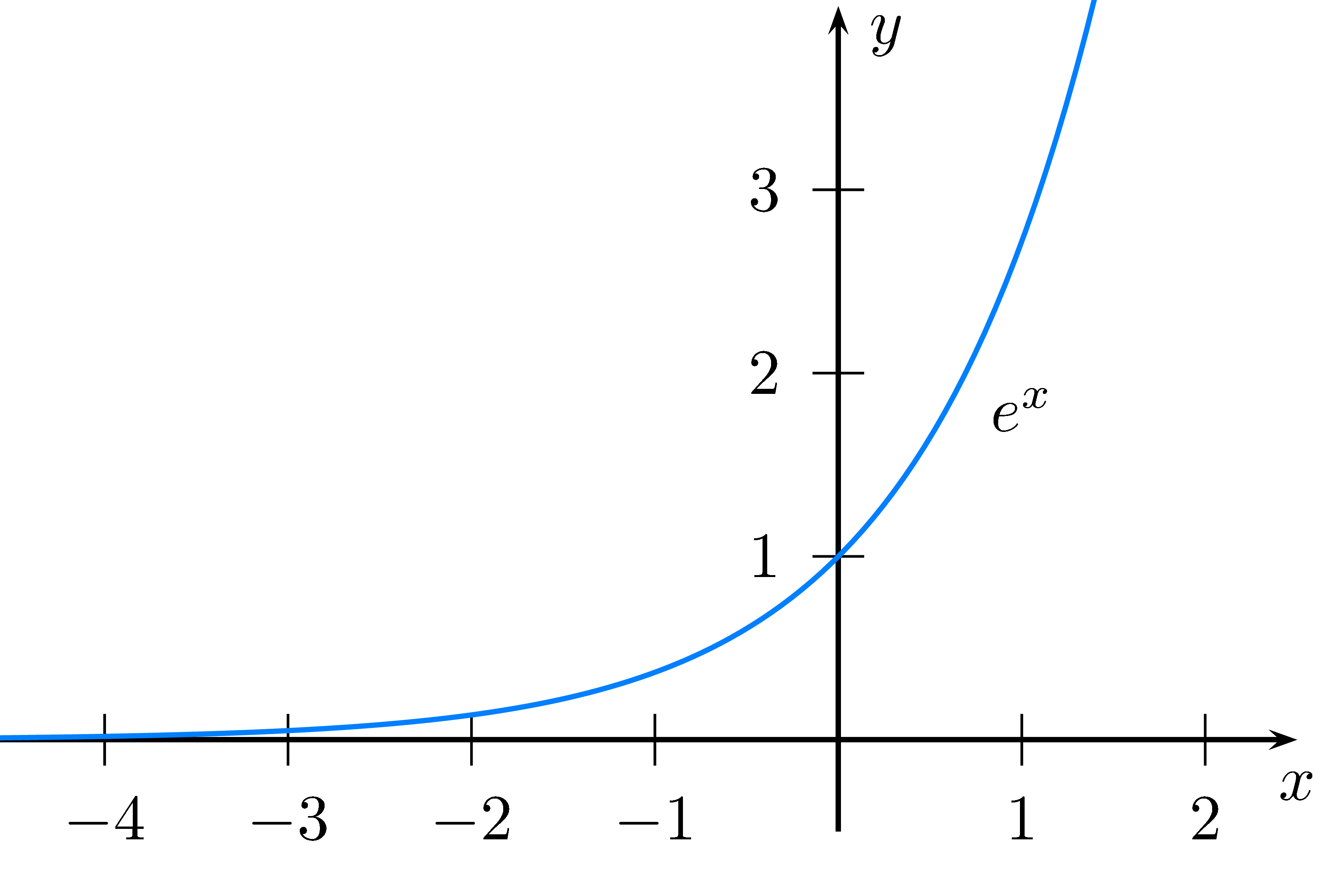
Der Graph von $f(x)=e^x$ geht für $x\rightarrow+\infty$ gegen $\infty$.
Für $x\rightarrow -\infty$ geht der Graph jedoch gegen 0.
Für $x\rightarrow -\infty$ geht der Graph jedoch gegen 0.
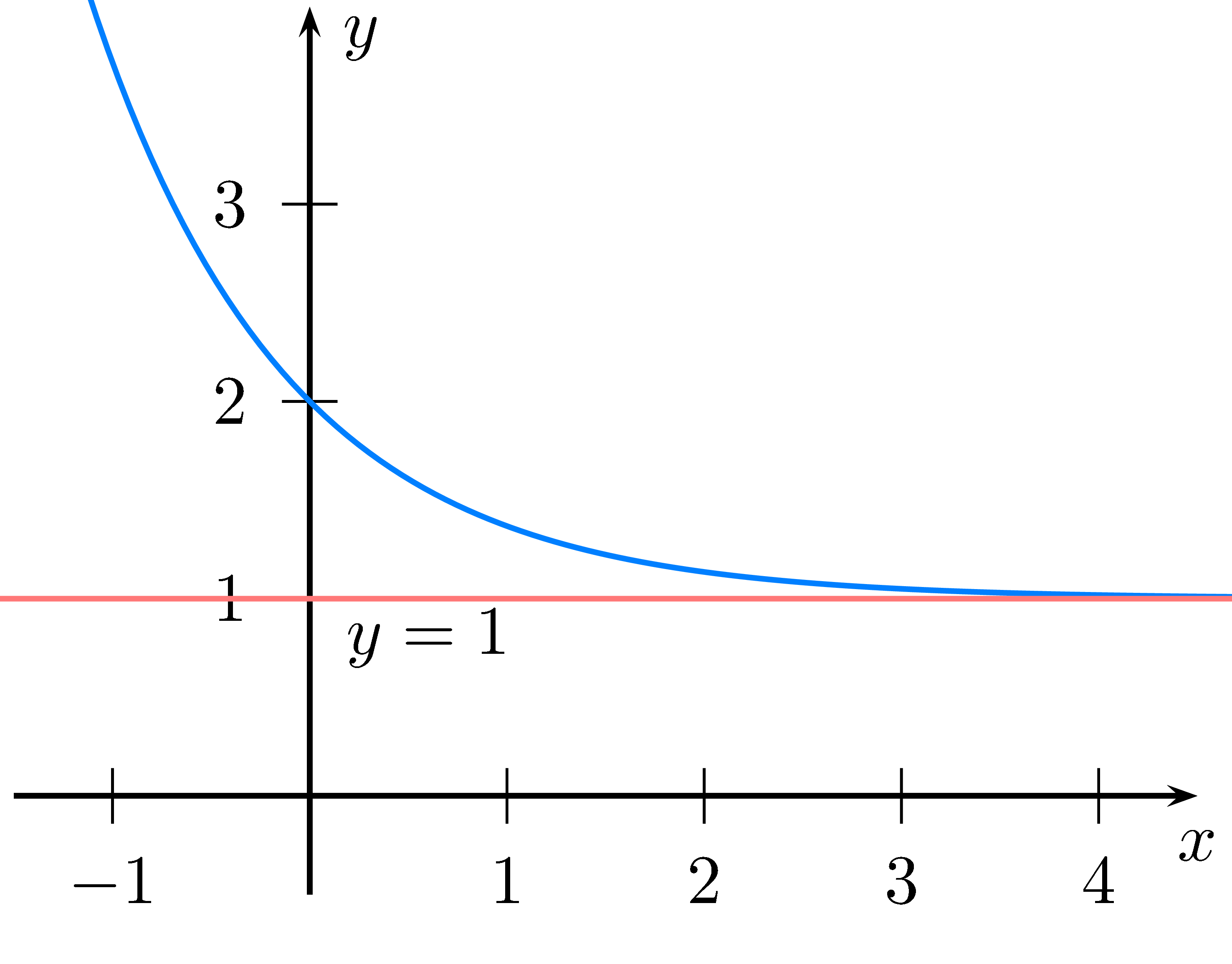
Da $e^x$ für $x\rightarrow -\infty$ gegen 0 geht, verhalten sich Exponential-Funktionen
für betragsmäßig große $x$ manchmal wie Geraden.
Solche Geraden nennt man Asymptoten. Eine Asymptote ist also eine Gerade an die sich das Schaubild der Funktion immer weiter annähert, wenn $x$ betragsmäßig größer wird.
Meist nähert sich eine Funktion nur auf einer Seite einer Asymptote an (also für $x\rightarrow-\infty$ oder $x\rightarrow\infty$).
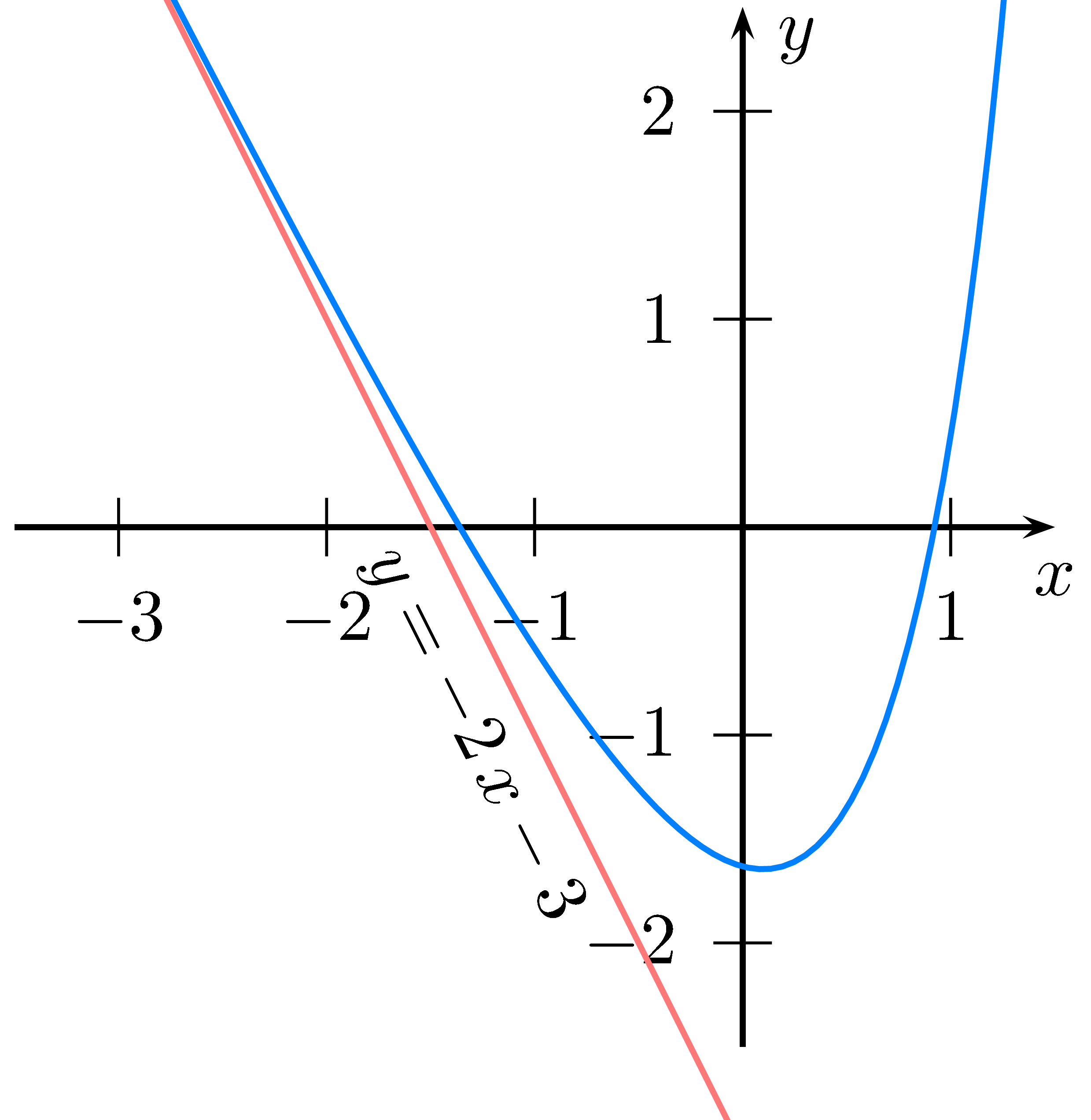
Manche $e$-Funktionen haben keine Asymptote.
Solche Geraden nennt man Asymptoten. Eine Asymptote ist also eine Gerade an die sich das Schaubild der Funktion immer weiter annähert, wenn $x$ betragsmäßig größer wird.
Meist nähert sich eine Funktion nur auf einer Seite einer Asymptote an (also für $x\rightarrow-\infty$ oder $x\rightarrow\infty$).
Manche $e$-Funktionen haben keine Asymptote.