- Gegeben ist $f(x)=300\cdot 2^x$
Der Anfangswert ist 300 und die Basis ist 2.
Da die Basis $2\gt 1$ wächst die Funktion, dass sieht man gut an der Wertetabelle.
Wird $x$ größer, so wird $f(x)$ größer
d.h. $f$ wächst$x$ -3 -2 -1 0 1 2 3 4 $f(x)$ 37,5 75 150 300 600 1200 2400 4800
und natürlich am Schaubild:
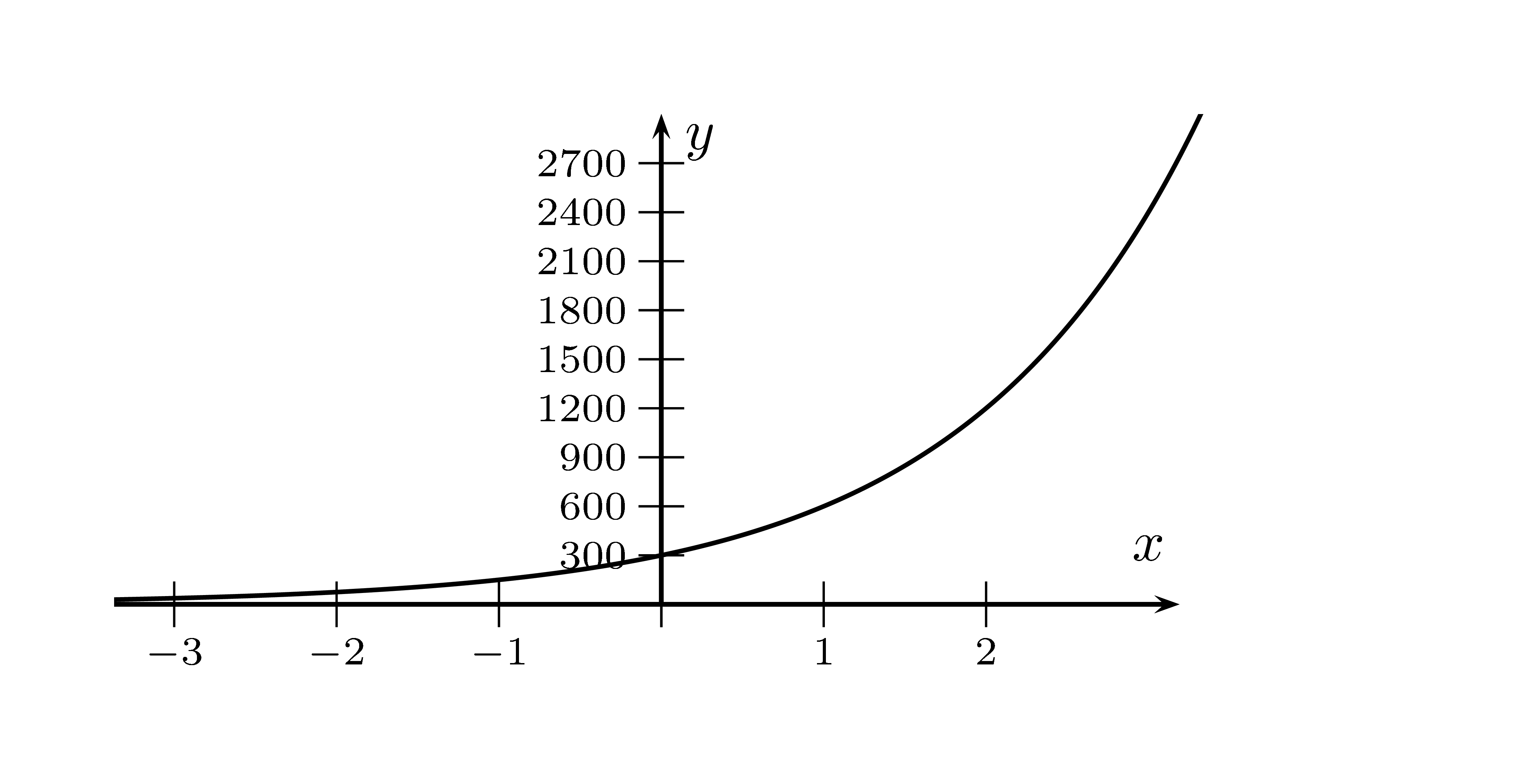
Der Graph von $f$. - Gegeben ist $f(x)=10\cdot 0{,}5^x$
Der Anfangswert ist 10 und die Basis ist 0,5.
Da die Basis $0{,}5\lt 1$ fällt die Funktion, dass sieht man gut an der Wertetabelle.
Wird $x$ größer, so wird $f(x)$ kleiner
d.h. $f$ fällt$x$ -3 -2 -1 0 1 2 3 4 $f(x)$ 80 40 20 10 5 2,5 1,25 0,625
und natürlich am Schaubild:
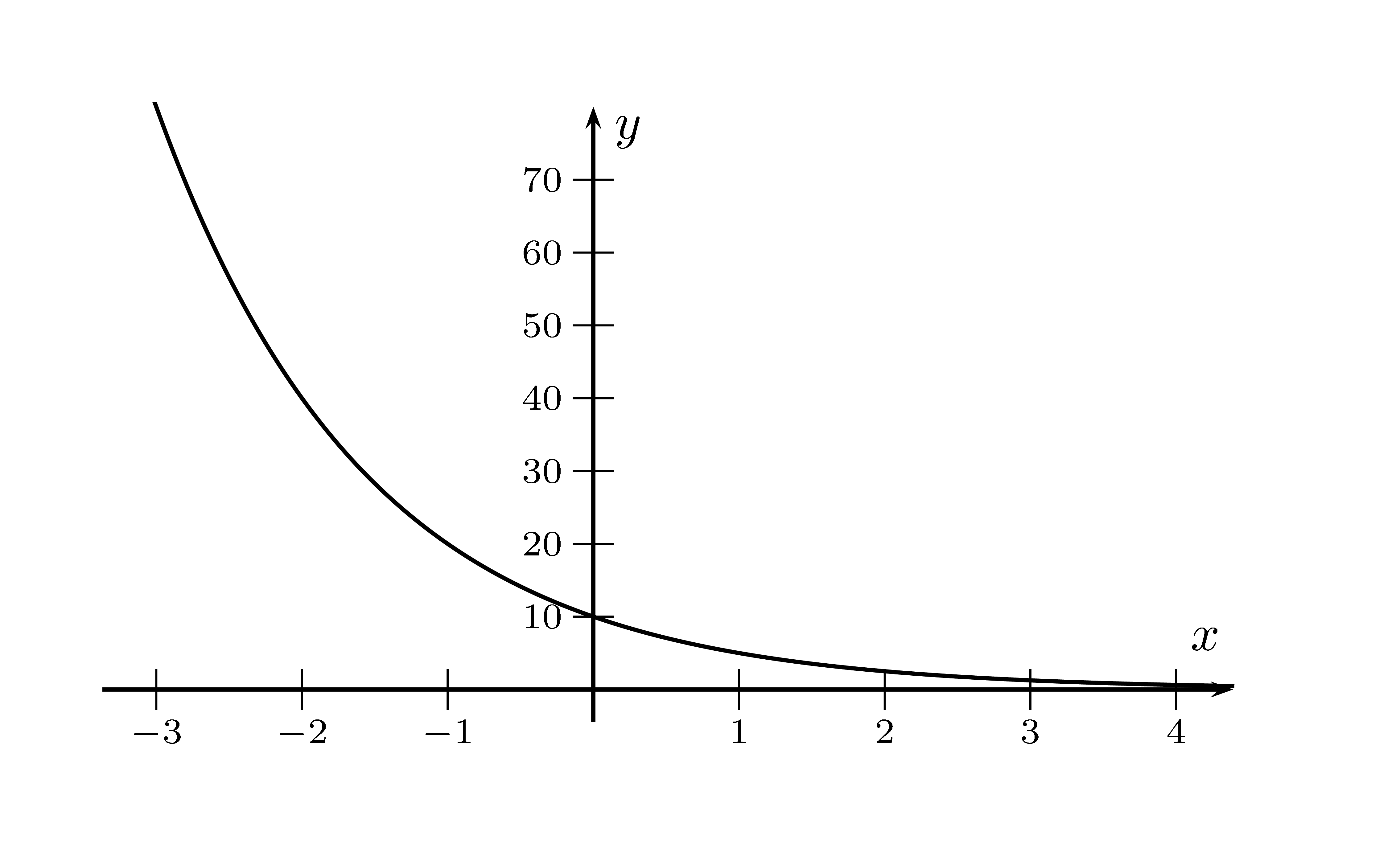
Der Graph von $f$.