Aufgabe 3
Eine Parabolantenne hat immer einen parabelförmigen Querschnitt.
Bestimmen Sie für eine Parabolantenne die einen Durchmesser von 100cm
und eine maximale Höhe von 25cm hat den Öffnungsfaktor a.
Hinweis
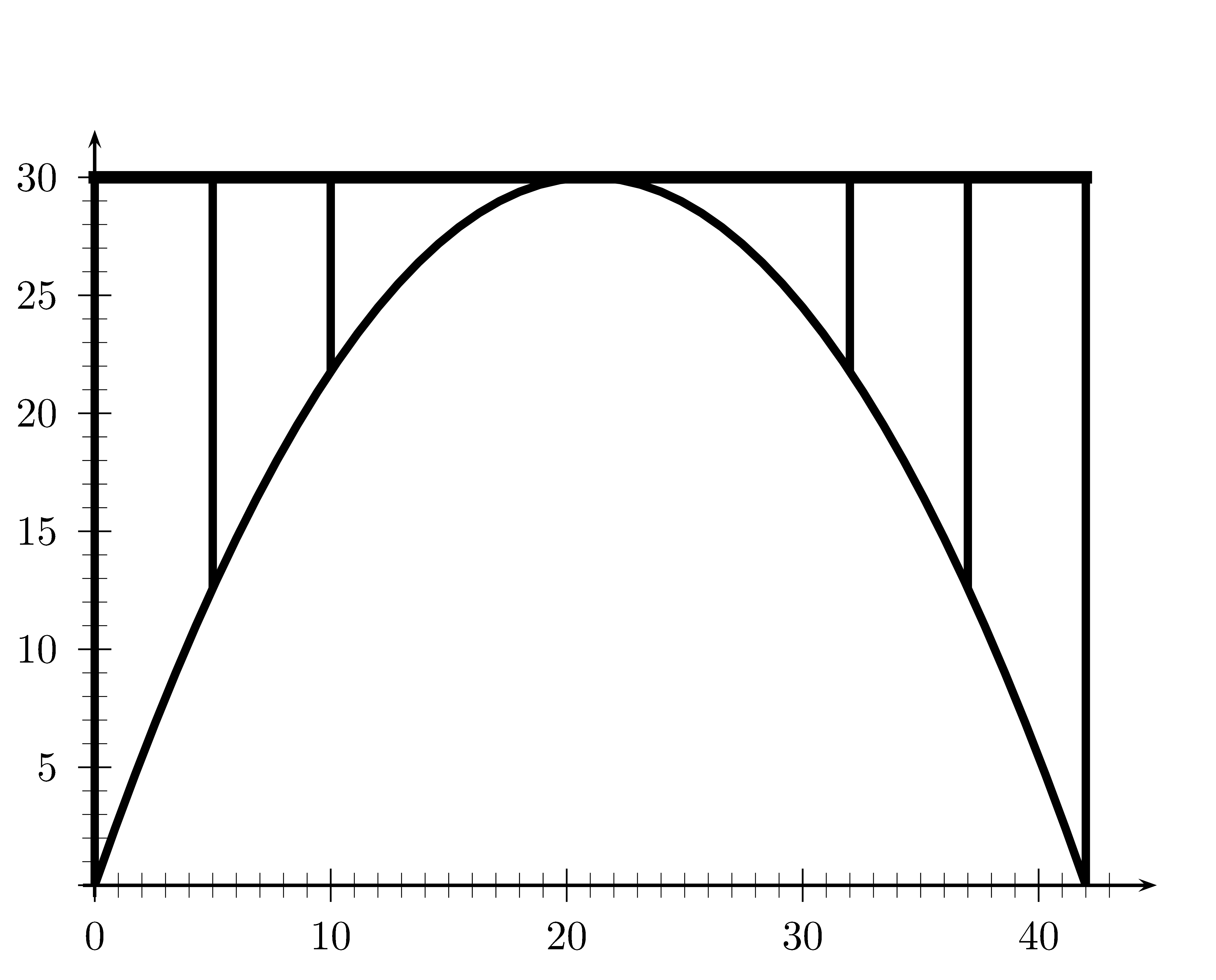
Zuerst braucht man ein Achsenkreuz.Entweder man legt es so, dass der Scheitel im Ursprung liegt (dann Scheitelform aufstellen)
oder man legt es so, dass die Enden auf der $x$-Achse liegen (dann Produktform aufsellen).