< Index
Steigung ablesen
Aufgabe 1 - Steigung und Funktionsgleichung
Bestimmen Sie die Steigung der Geraden von folgenden Funktionen:
- $f(x)=3x+1$
Lösung
3 da hier 3 mal $x$ steht
- $f(x)=1-2x$
Lösung
-2, da hier -2 mal $x$ steht
- $f(x)=4(x-3)$
Lösung
4, da hier 4 mal $x$ steht
Ausmultipliziert: 4x-12
- $f(x)=x-2$
Lösung
1, da hier 1 mal $x$ steht
Die 1 steht zwar nicht da, aber $1\cdot x=x$.
- $f(x)=-x+\frac12$
Lösung
-1, da hier -1 mal $x$ steht
Die -1 steht zwar nicht da, aber $(-1)\cdot x=-x$.
- $f(x)=2x+\frac78+3x$
Lösung
$m=5$, wenn man zusammenfasst erhält man: $f(x)=5x+\frac78$
- $f(x)=x+x+x-1$
Lösung
$m=3$, wenn man zusammenfasst erhält man: $f(x)=3x-1$
- $f(x)=-1$
Lösung
$m=0$, denn $f(x)=0\,x-1$
- $f(x)=4-2$
Lösung
$m=0$, denn $f(x)=0\,x+2$
Hier ist ja kein $x$ drin.
Aufgabe 2 - Steigung und Schaubild
Lesen Sie die Steigung der Geraden ab.
-
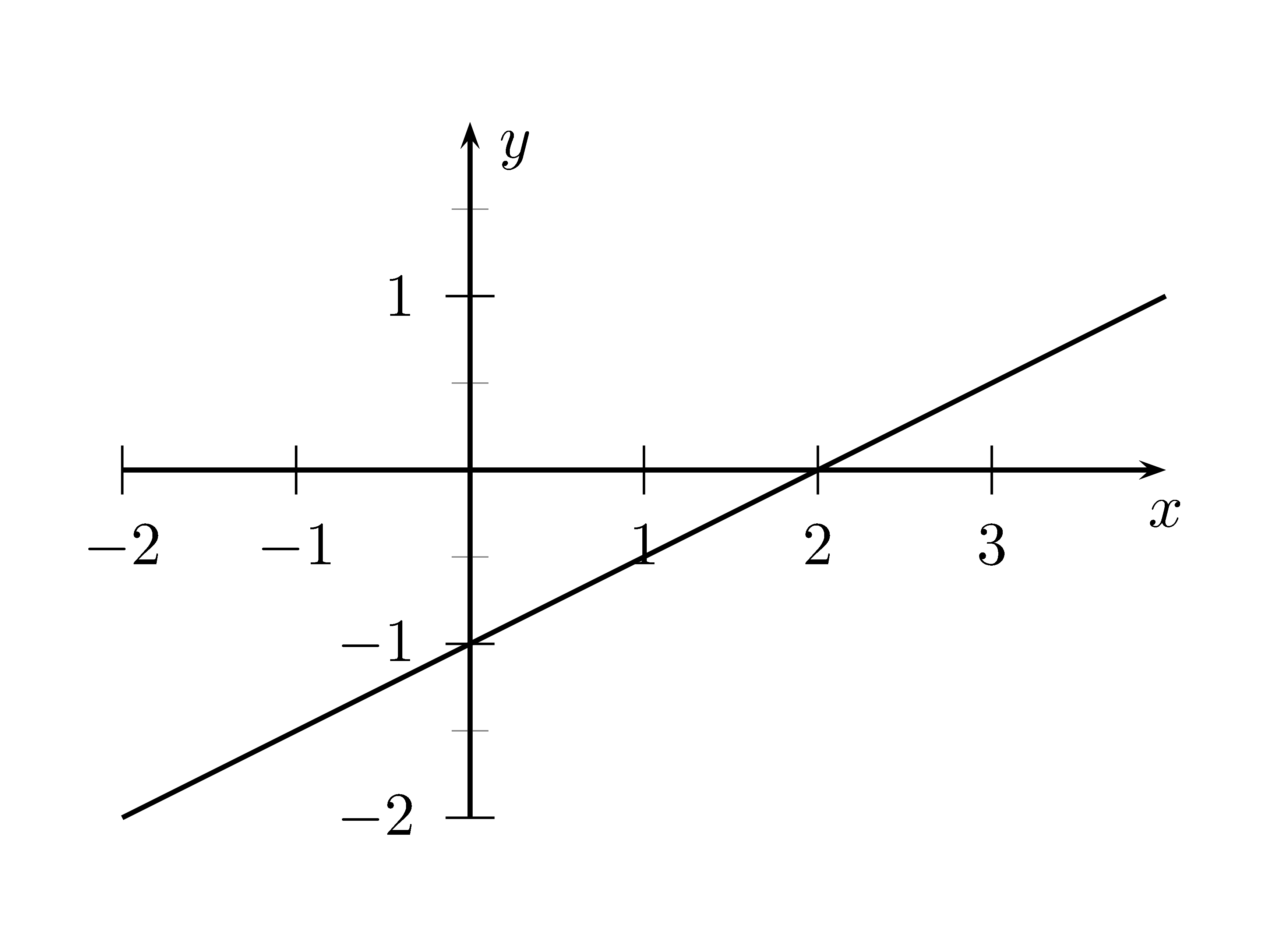
Lösung
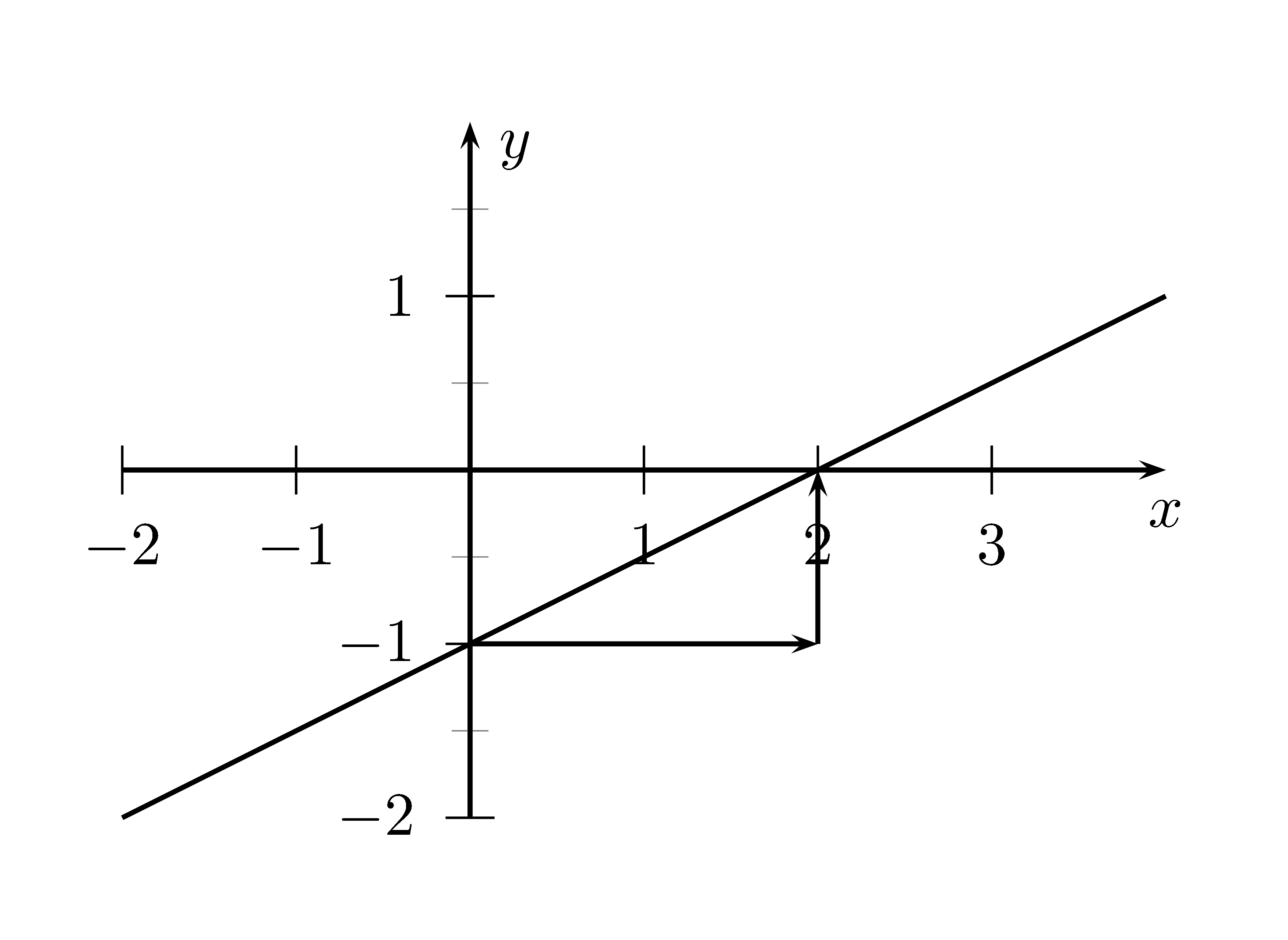 Steigungsdreieck von $x=0$ bis $x=2$ liefert die Steigung $m=\frac12$, denn $m=\frac{0-(-1)}{2-0}=\frac12$
Steigungsdreieck von $x=0$ bis $x=2$ liefert die Steigung $m=\frac12$, denn $m=\frac{0-(-1)}{2-0}=\frac12$
-
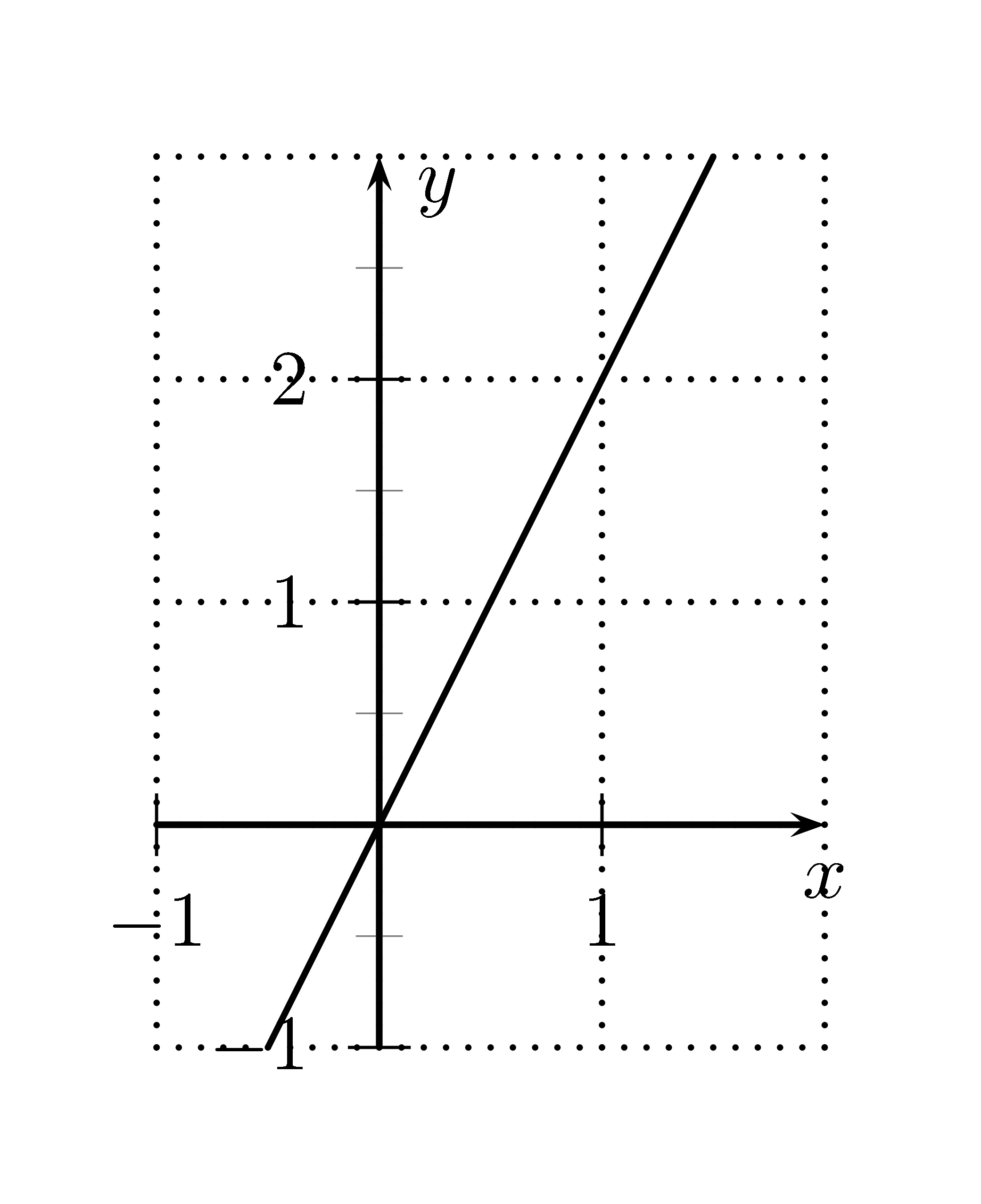
Lösung
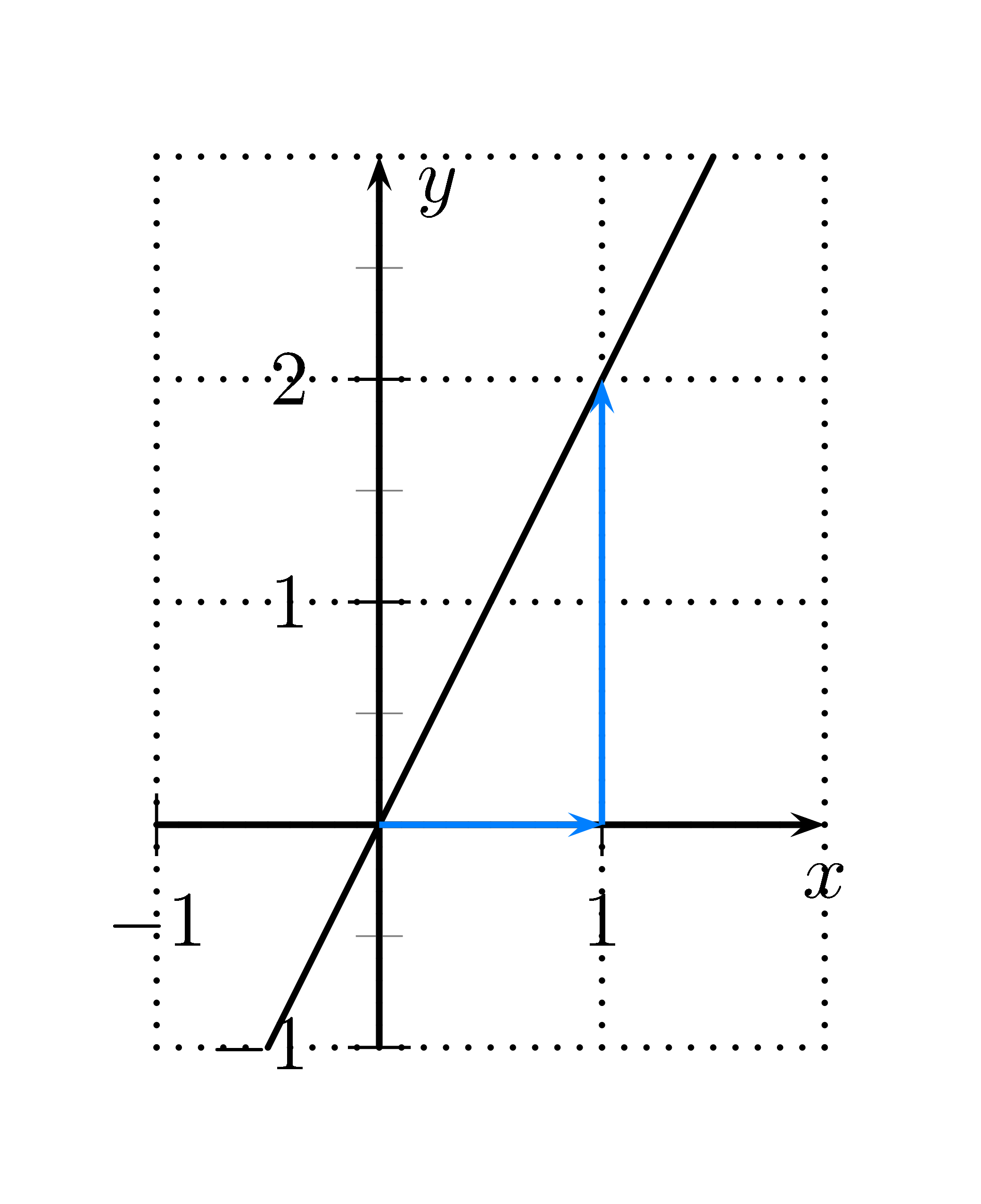 Steigungsdreieck von $x=0$ bis $x=1$ liefert die Steigung $m=2$, denn $m=\frac{2-0}{1-0}=2$
Steigungsdreieck von $x=0$ bis $x=1$ liefert die Steigung $m=2$, denn $m=\frac{2-0}{1-0}=2$
-
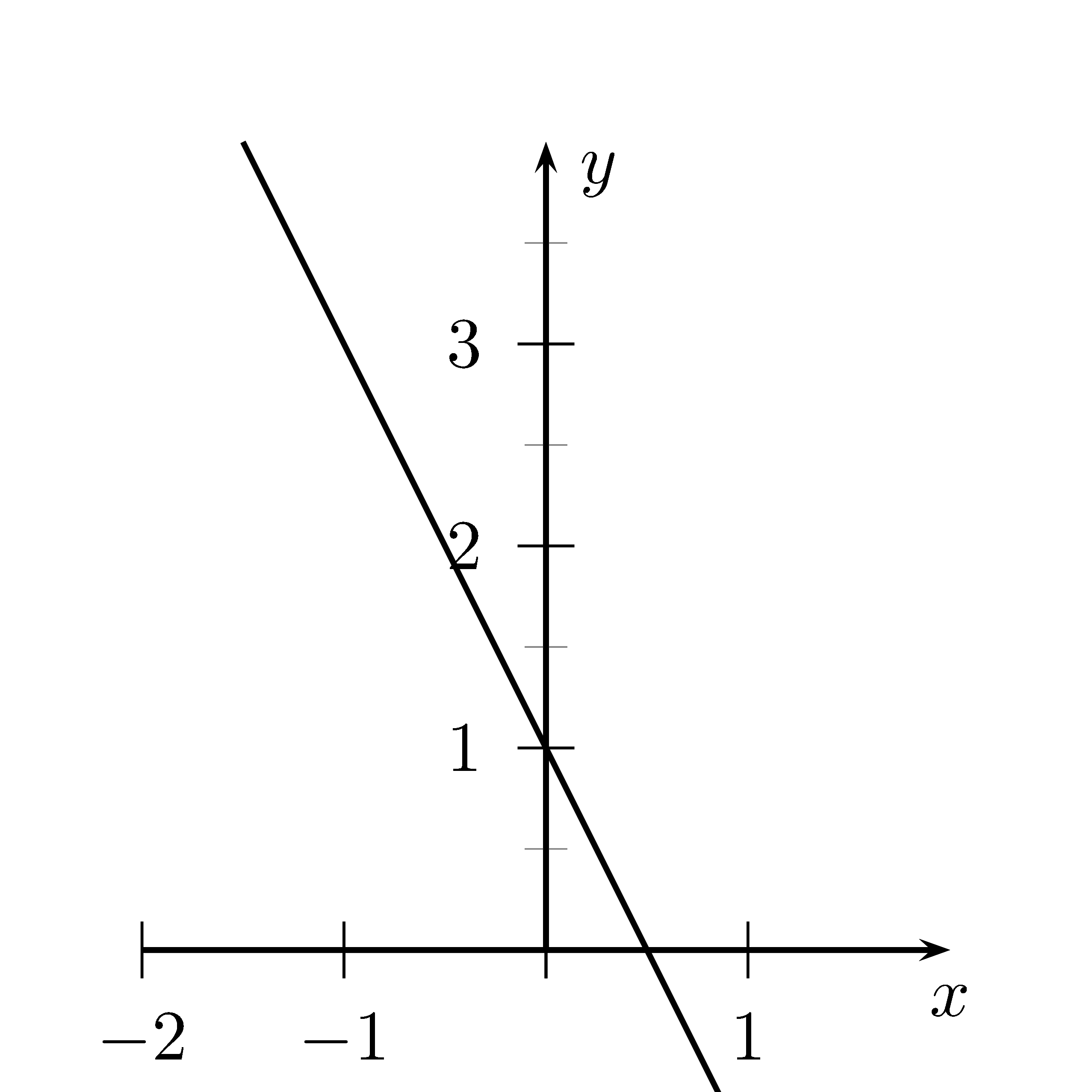
Lösung
 Steigungsdreieck von $x=-1$ bis $x=0$ liefert die Steigung $m=-2$, denn $m=\frac{3-1}{-1-0}=-2$
Steigungsdreieck von $x=-1$ bis $x=0$ liefert die Steigung $m=-2$, denn $m=\frac{3-1}{-1-0}=-2$
-
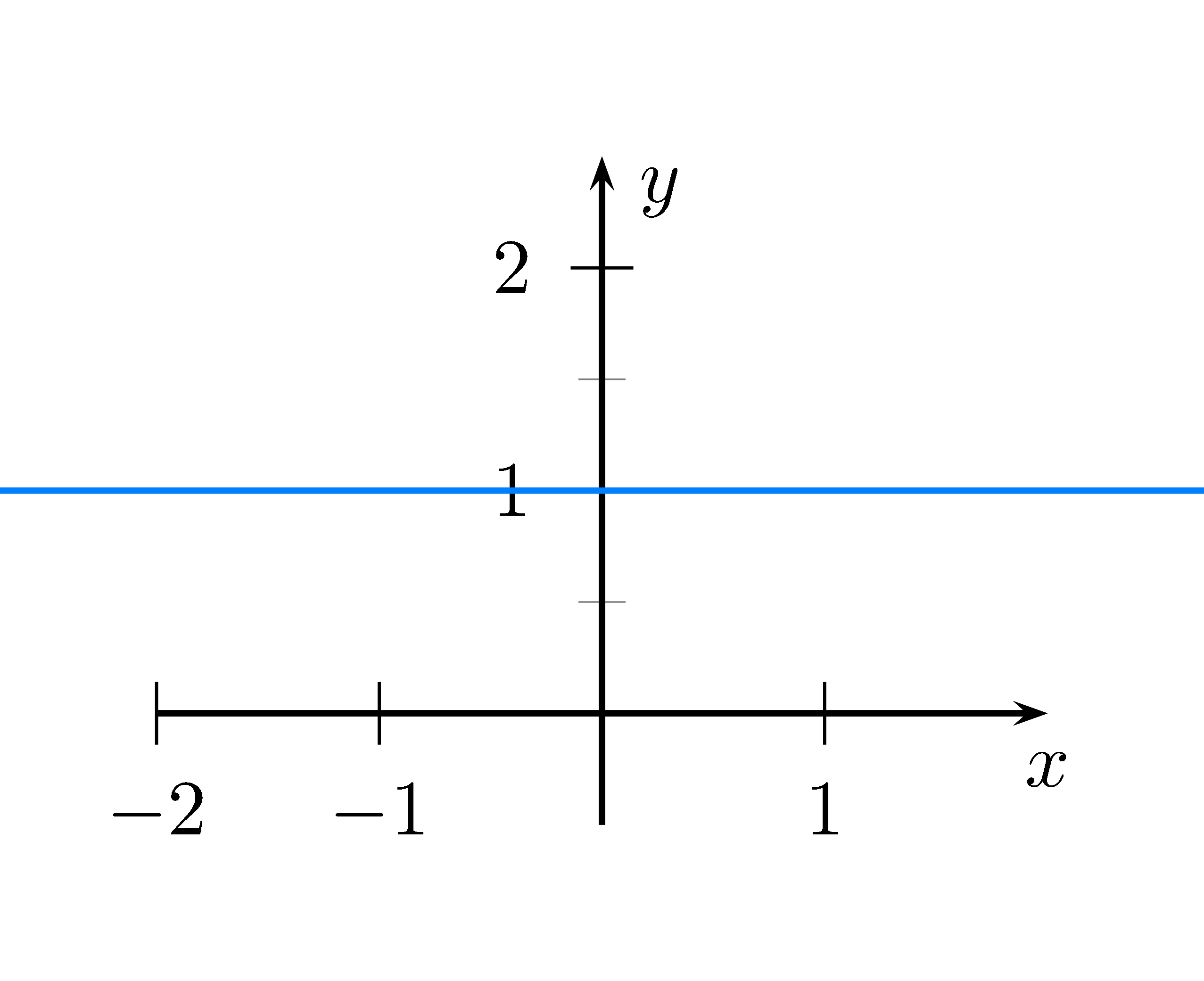
Lösung
Steigung ist 0, da die Gerade waagerecht ist
-
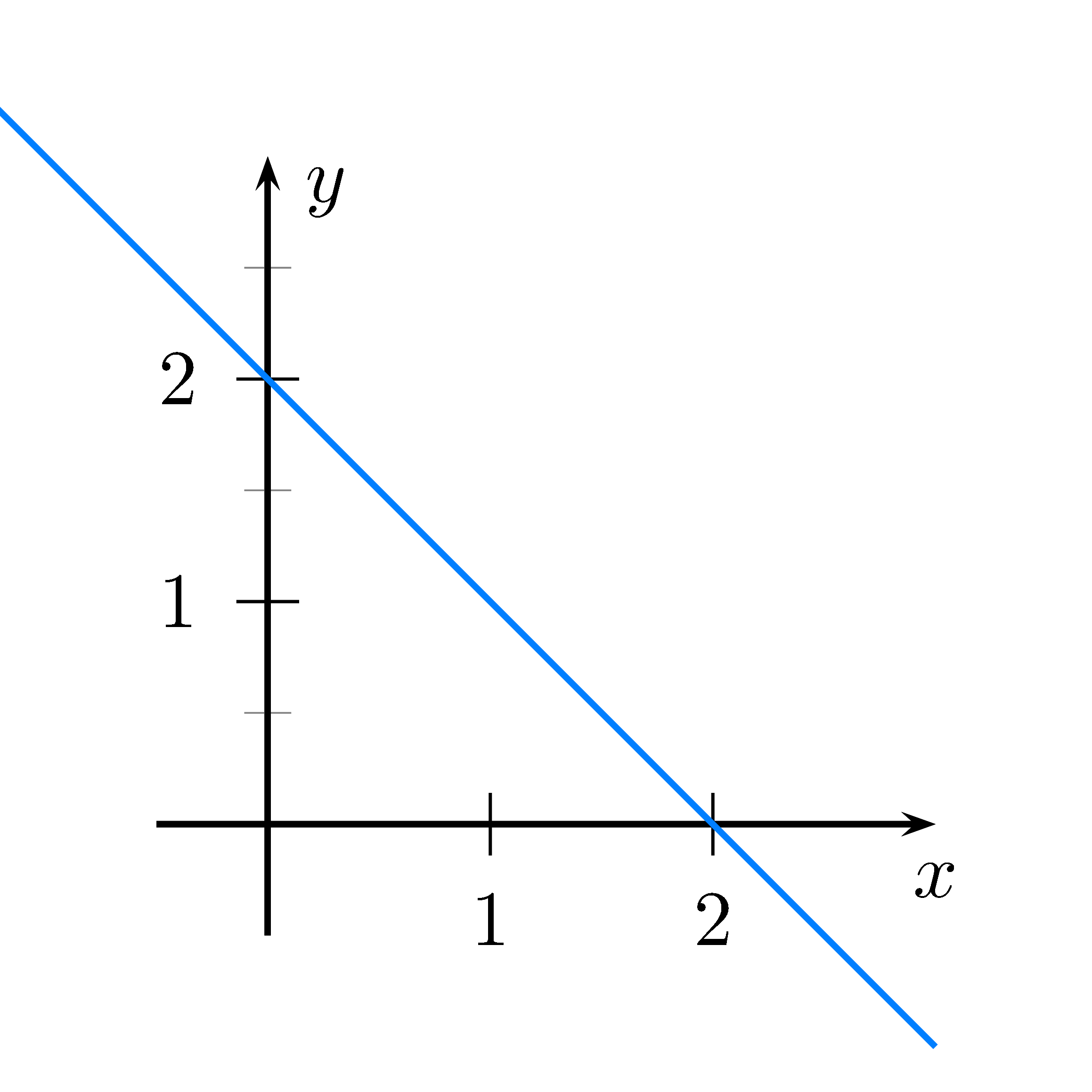
Lösung
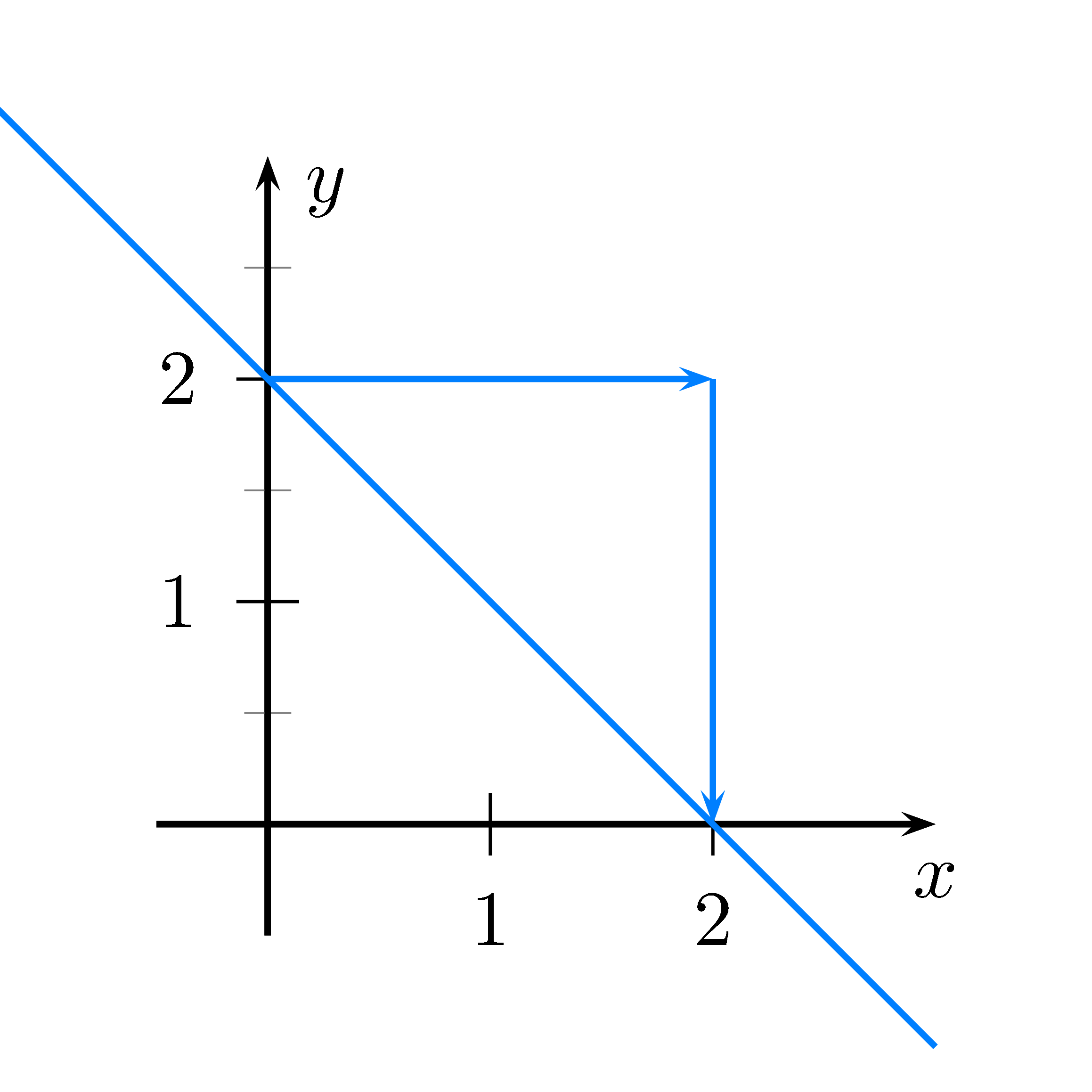 Steigung ist -1
Steigung ist -1
-
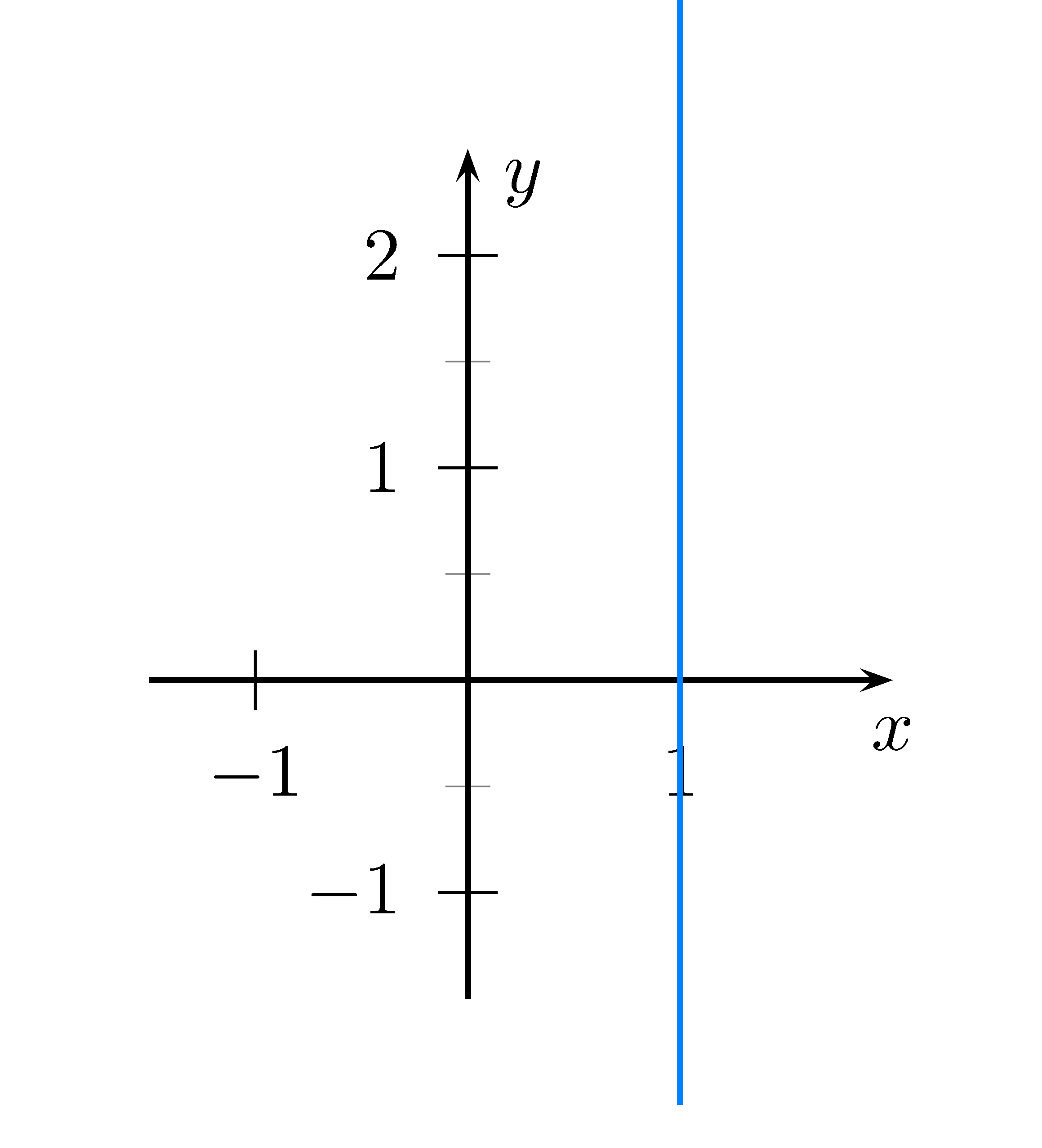
Lösung
Dies ist die Senkrechte $x=1$, sie ist keine Funktion :)