Geraden

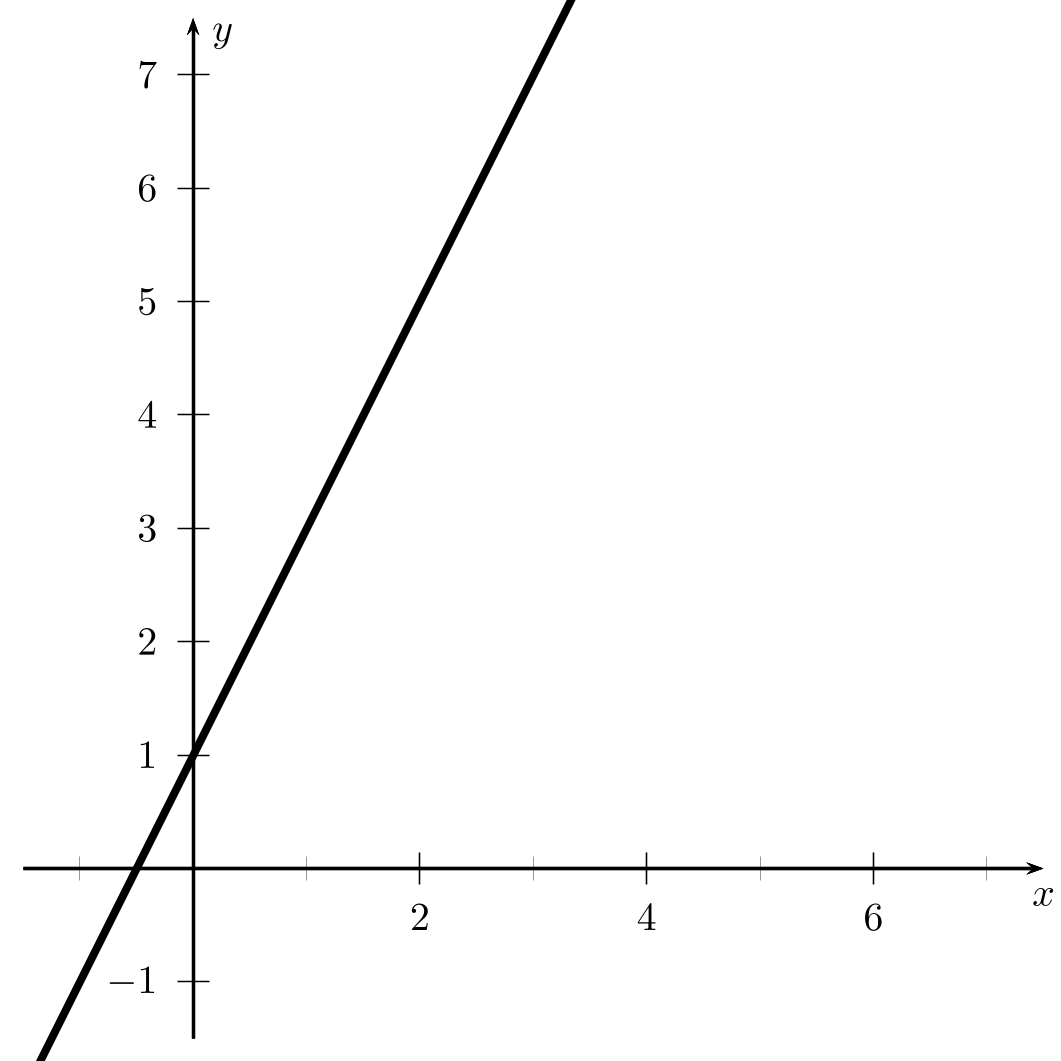
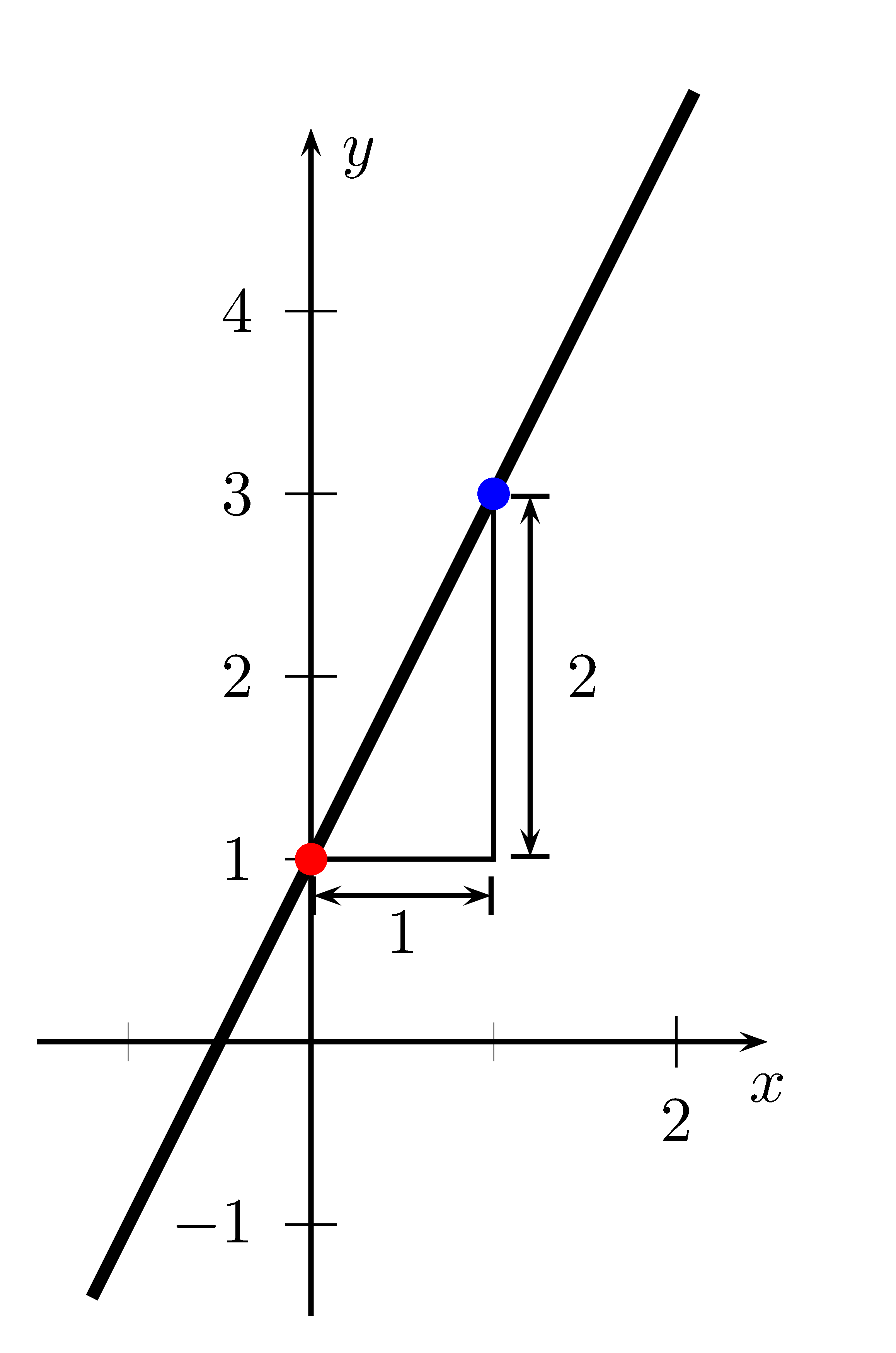
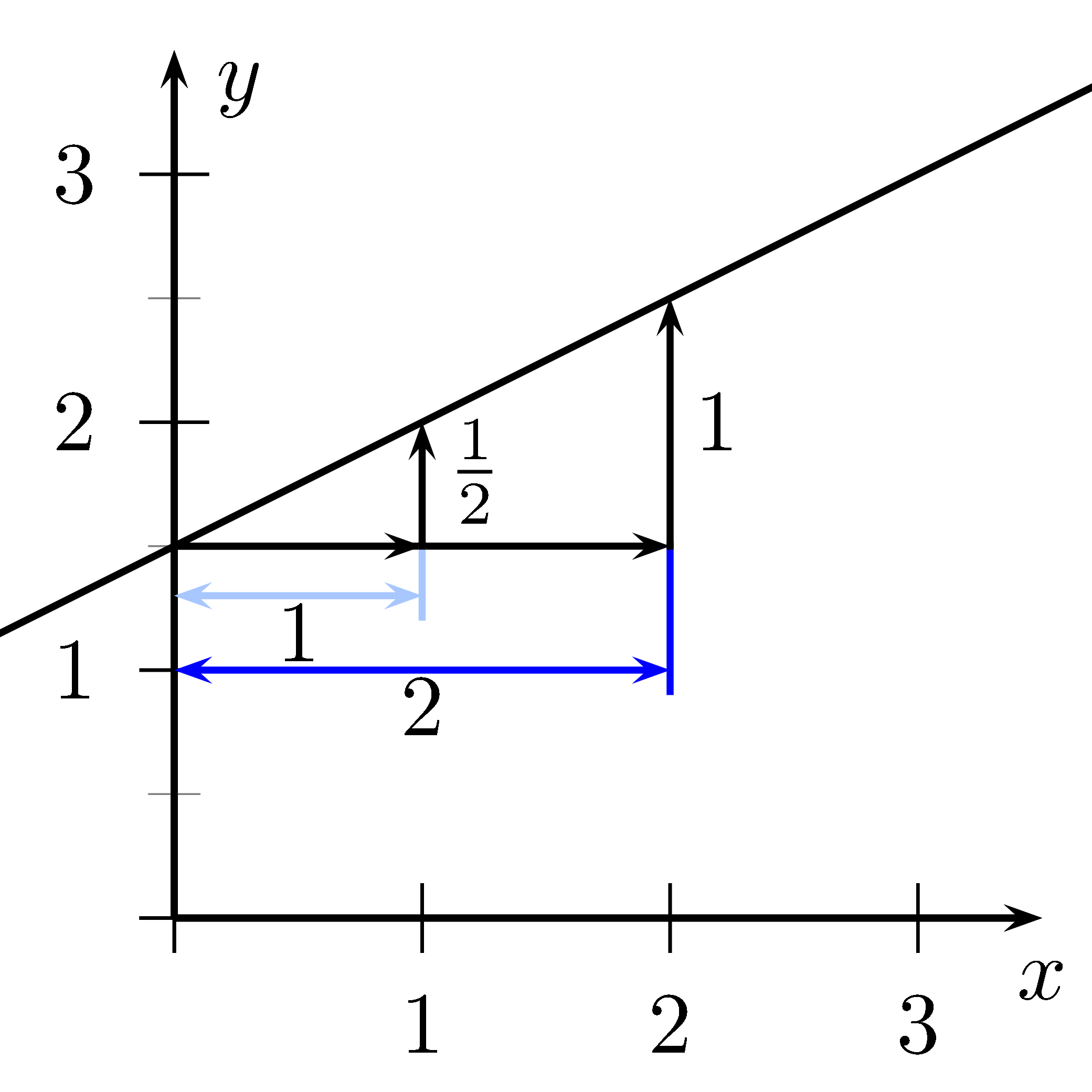
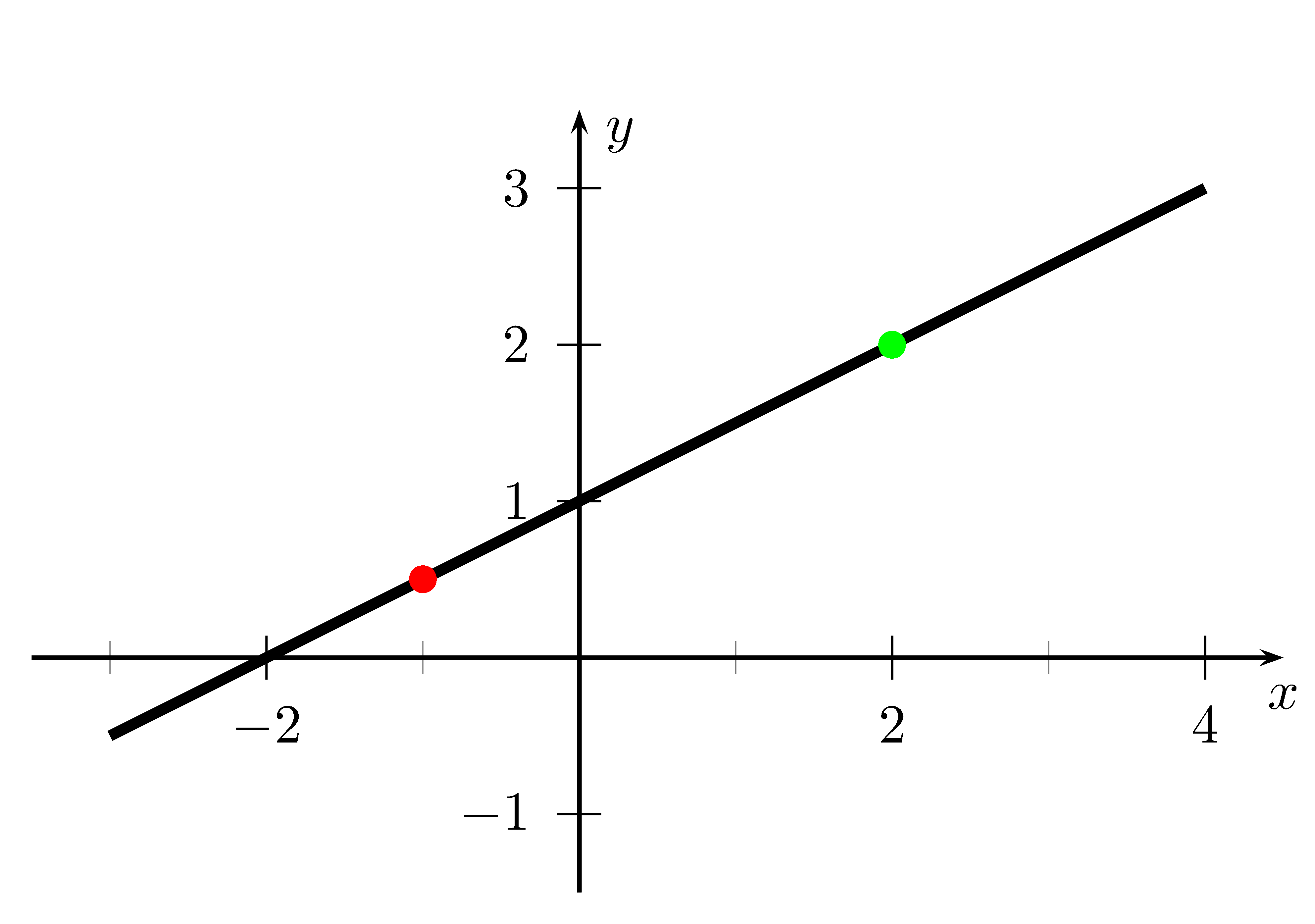
Eine Gerade ist das Schaubild einer linearen Funktion.
In einem kartesischen Koordinatensystem sind die Punkte $(x\mid y)$ einer Geraden genau die Lösungen der Gleichung $y=mx+b$.
Das heißt jeder Punkt $(x\mid f(x))$ ist Teil der Geraden.
Bsp.: Die Gerade der linearen Funktion $f(x)=2x-1$ enthält die Punkte $(-2\mid -5)$, $(-1\mid -3)$, $(0\mid -1)$, $(1\mid 1)$, $(2\mid 3)$ und $(3\mid 5)$.

Eine tabellarische Auflistung dieser Punkte nennt man Wertetabelle

$\begin{array}{c|c} x & y=f(x) \\\hline -2 & -5 \\\hline -1 & -3 \\\hline 0 & -1 \\\hline 1 & 1 \\\hline 2 & 3 \\\hline 3 & 5 \\\hline 4 & 7 \\\hline \end{array}$
oder waagerecht
$\begin{array}{c||r|r|r|r|r|r|r|} x & -2 & -1 & 0 & 1 & 2 & 3 & 4 \\\hline y=f(x) & -5 & -3 & -1 & 1 & 3 & 5 & 7 \\ \end{array}$

Zeichnen

Mittels $b$ und $m$

Um die Geraden der linearen Funktion $f(x)=mx+b$ zu zeichnen beginnt man an der $y$-Achse bei $b$ (also dem Punkt $(0\mid b)$).
Von hieraus geht man eins nach rechts und um $m$ nach oben (wenn $m\lt 0$, nach unten).
Ist $m$ sehr klein (z.B. 0,3), kann man um $k$ nach rechts gehen und um $k\cdot m$ nach oben.
Besonders bei Brüchen, also z.B. $m=\frac13$, kann man um den Nenner (hier 3) nach rechts und um den Zähler (hier 1, da $3\cdot \frac13 = 1$) nach oben gehen.

Bsp.: Gegeben ist die Funktion $f(x)=\frac12x+1{,}5$. Gesucht ist die zugehörige Gerade.
Man beginnt bei $(0\mid 1{,}5)$ und geht 1 nach rechts und $\frac12$ nach oben. Im Schaubild ergibt dieser Weg das erste Steigungsdreieck.

Oder man beginnt bei $(0\mid 1{,}5)$ und geht 2 nach rechts und $2\cdot\frac12=1$ nach oben. Im Schaubild ergibt dieser Weg das zweite Steigungsdreieck.
Der Vorteil von breiteren Steigungsdreiecken ist, dass sich zeichnerische Ungenauigkeiten weniger auswirken.
Versuchen Sie es: Zeichnen Sie die gleiche Gerade mit einem Steigungsdreieck, dass 5mm, 1cm und 2cm breit ist. Nehmen Sie den Punkt bei $x=4$, um zu überprüfen um wie viel sie ihn verfehlen.

Gerade mit 2 Steigungsdreiecken (klein und groß) — 2 unterschiedlich
breite Steigungsdreiecke

Mittels 2 Punkten

Berechnet man zwei Punkte der Gerade (also zu zwei $x$-Werten, den zugehörigen Funktionswert $f(x)$ ) und zeichnet diese ins Koordinatensystem ein, so ist die Gerade durch diese zwei Punkte das Schaubild von $f(x)$.

Hat man zu einer Funktion bereits die zugehörige Wertetabelle, so kann man aus ihr zwei Punkte auslesen, um die Funktion zu zeichnen.
Die Wertetabelle kann man sich auch vom WTR erstellen lassen.

Bsp: Gegeben ist die Funktion $f(x)=\frac12x+1$
Um das Schaubild dieser Funktion zu zeichnen berechnen man $f(-1)=\frac12$ und $f(2)=2$.
Nun zeichnen man die Punkte $\left(0\mid \frac12\right)$ und $(2\mid 2)$ in das Koordinatensystem ein.
Die Gerade durch diese Punkte zieht man mit einem Lineal.
Fertig.

Spezielle Geraden

Waagerechte Geraden, also Schaubilder von Funktionen $f(x)=b$, sind leicht zu zeichnen. Sie sind einfach waagerechte Linien auf Höhe $b$.

Bsp.: Das Schaubild $K_f$ der Funktion $f(x)=2$ soll gezeichnet werden.
Hierzu legt man das Lineal parallel zur $x$-Achse an und zwar so, dass es bei der $y$-Achse durch 2 geht.
Dann zieht man mit dem Bleistift eine waagerechte Linie am Lineal entlang.

Ursprungsgeraden, also Geraden von Funktionen der Art $f(x)=mx$, zeichnet man wie normale Geraden.
Da hier der $y$-Achsenabschnitt $b=0$ ist, beginnt man mit dem Steigungsdreieck im Ursprung.
Will man Ursprungsgeraden mittels zwei Punkten zeichnen, so ändert sich nichts am oben beschriebenen Vorgehen: Man berechnet zwei $y$-Werte und zeichnet die Gerade durch diese Punkte im Koordinatensystem.