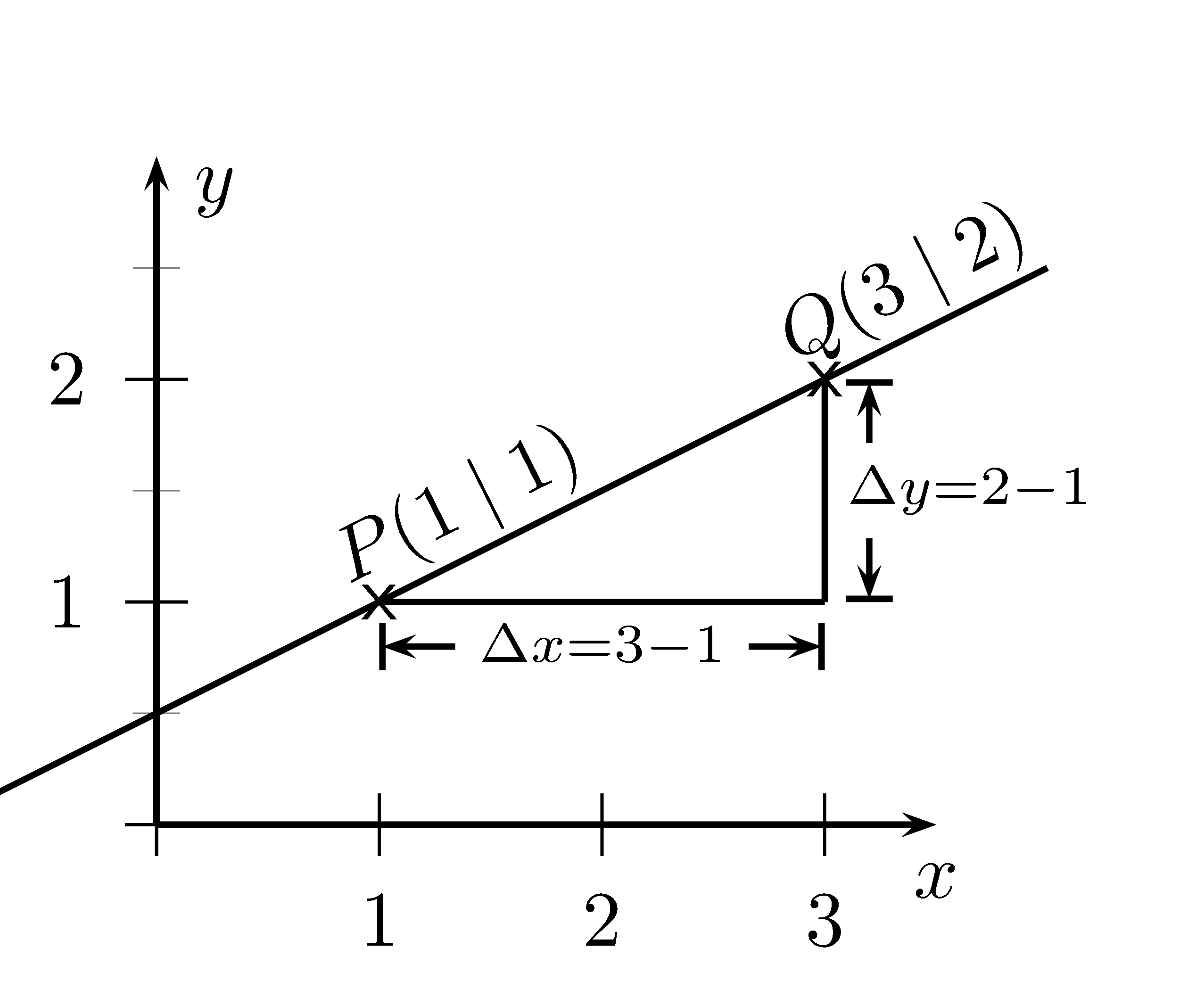
Sind zwei Punkte $P(x_1|y_1)$ und $Q(x_2|y_2)$ auf einer Geraden gegeben,
so ist die Steigung $m=\dfrac{\Delta y}{\Delta x}=\dfrac{y_2-y_1}{x_2-x_1}$.
$\Delta y$ ist die Differenz der $y$-Koordinaten der Punkte und $\Delta x$ ist die Differenz der $x$-Koordinaten. Die beiden Werte $\Delta x$ und $\Delta y$ sind also die Kathetenlängen eines Steigungsdreiecks der gesuchten Geraden.
Da gilt $m=\tan(\alpha)$ ist $m=\dfrac{\Delta y}{\Delta x}$, da Gegenkathete durch Ankathete der Tangens ist.
Nachdem man $m$ bestimmt hat, stellt man die Geradengleichung mittels $m$ und einem der Punkte auf (z.B. $P$).
$\Delta y$ ist die Differenz der $y$-Koordinaten der Punkte und $\Delta x$ ist die Differenz der $x$-Koordinaten. Die beiden Werte $\Delta x$ und $\Delta y$ sind also die Kathetenlängen eines Steigungsdreiecks der gesuchten Geraden.
Da gilt $m=\tan(\alpha)$ ist $m=\dfrac{\Delta y}{\Delta x}$, da Gegenkathete durch Ankathete der Tangens ist.
Nachdem man $m$ bestimmt hat, stellt man die Geradengleichung mittels $m$ und einem der Punkte auf (z.B. $P$).