Eine Funktion ordnet jedem $x$-Wert aus der Definitionsmenge einen $y$-Wert aus der
Wertemenge zu.
Diese Zuordnung von $x$ und $y$ kann man auch graphisch darstellen, da graphische Darstellungen oft intuitiver erfassbar sind als formale Darstellungen.
Einen Wert haben wir durch einen Punkt auf einem Zahlenstrahl dargestellt. Da wir jetzt zwei Werte haben, nämlich einen für $x$ und einen für $y$, könnten wir einfach zwei Zahlenstrahle verwenden. Jedes Paar $(x\mid y)$ kann dann als Pfeil von dem einen Zahlenstrahl zum anderen Zahlenstrahl darstellen.
Diese Zuordnung von $x$ und $y$ kann man auch graphisch darstellen, da graphische Darstellungen oft intuitiver erfassbar sind als formale Darstellungen.
Einen Wert haben wir durch einen Punkt auf einem Zahlenstrahl dargestellt. Da wir jetzt zwei Werte haben, nämlich einen für $x$ und einen für $y$, könnten wir einfach zwei Zahlenstrahle verwenden. Jedes Paar $(x\mid y)$ kann dann als Pfeil von dem einen Zahlenstrahl zum anderen Zahlenstrahl darstellen.
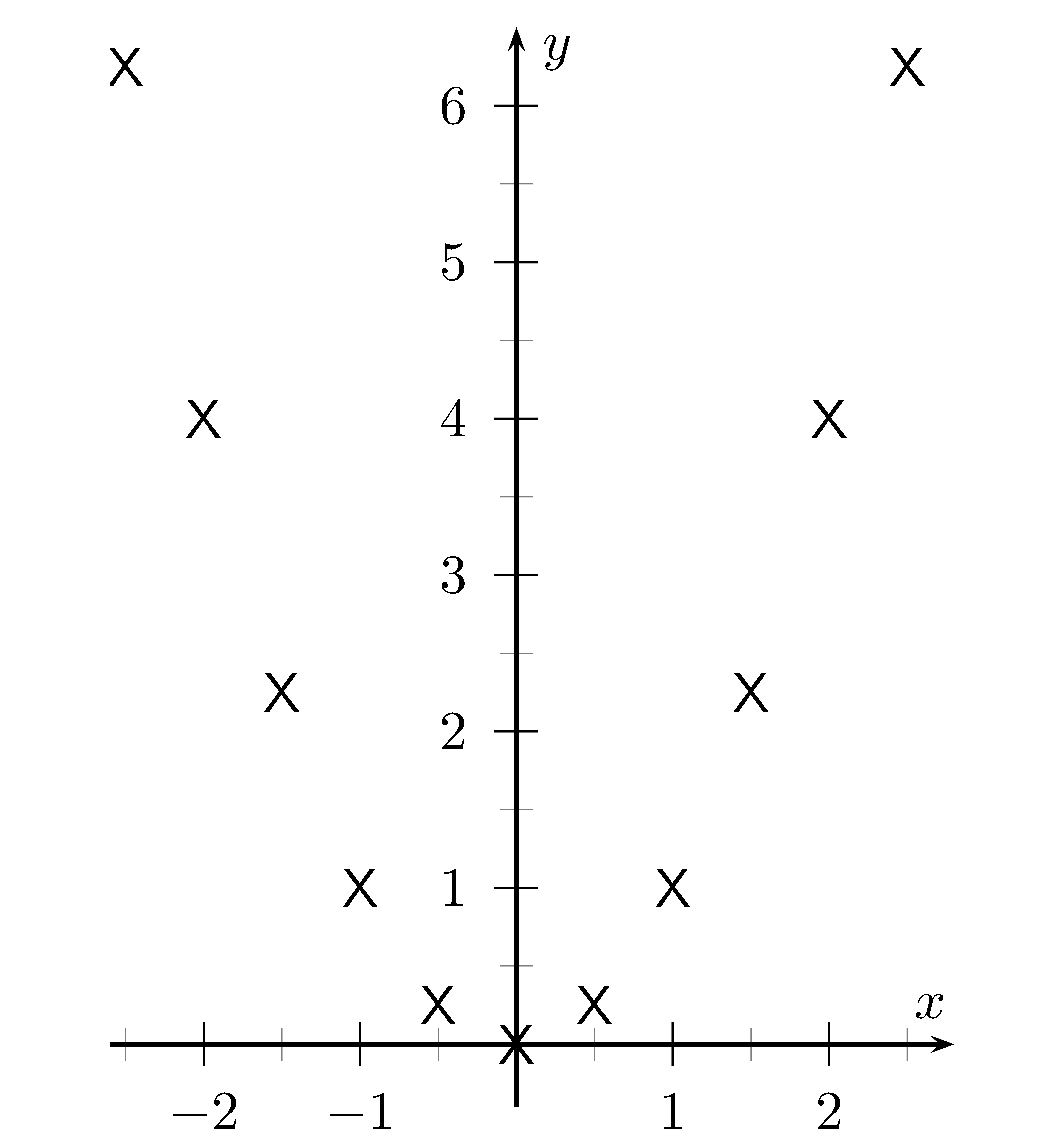
Allerdings wird diese Darstellung schnell unübersichtlich, wie man am Beispiel der
Normalparabel $y=x^2$ sieht.
Wenn man für viele $x$ die Pfeile einzeichnet wird die Darstellung sehr schnell überladen und unübersichtlich.
Wenn man für viele $x$ die Pfeile einzeichnet wird die Darstellung sehr schnell überladen und unübersichtlich.